Modern Methods for the Computation of Scattering Amplitudes
Giuseppe De Laurentis
LTP Seminar

Find these slides at gdelaurentis.github.io/slides/psi-ltp-seminar
Introduction
Amplitudes and Cross Sections
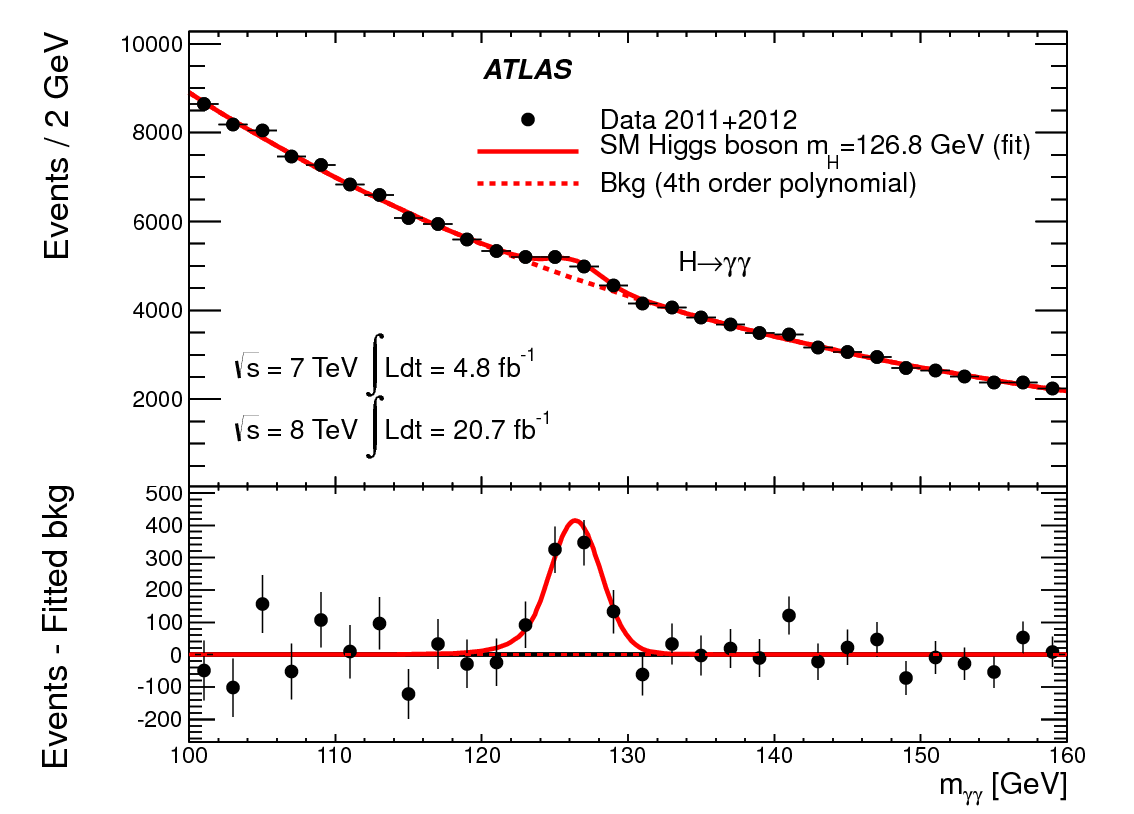
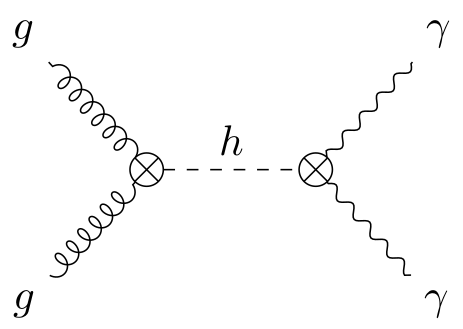 $$\mathcal{A}_{pp\rightarrow h \rightarrow \gamma\gamma} \sim \frac{1}{m_{\gamma\gamma}^2 - m^2_h + i m_h \Gamma_h}$$
$$\Rightarrow\; \text{Breit–Wigner distribution}$$
$$\mathcal{A}_{pp\rightarrow h \rightarrow \gamma\gamma} \sim \frac{1}{m_{\gamma\gamma}^2 - m^2_h + i m_h \Gamma_h}$$
$$\Rightarrow\; \text{Breit–Wigner distribution}$$
Perturbation Theory
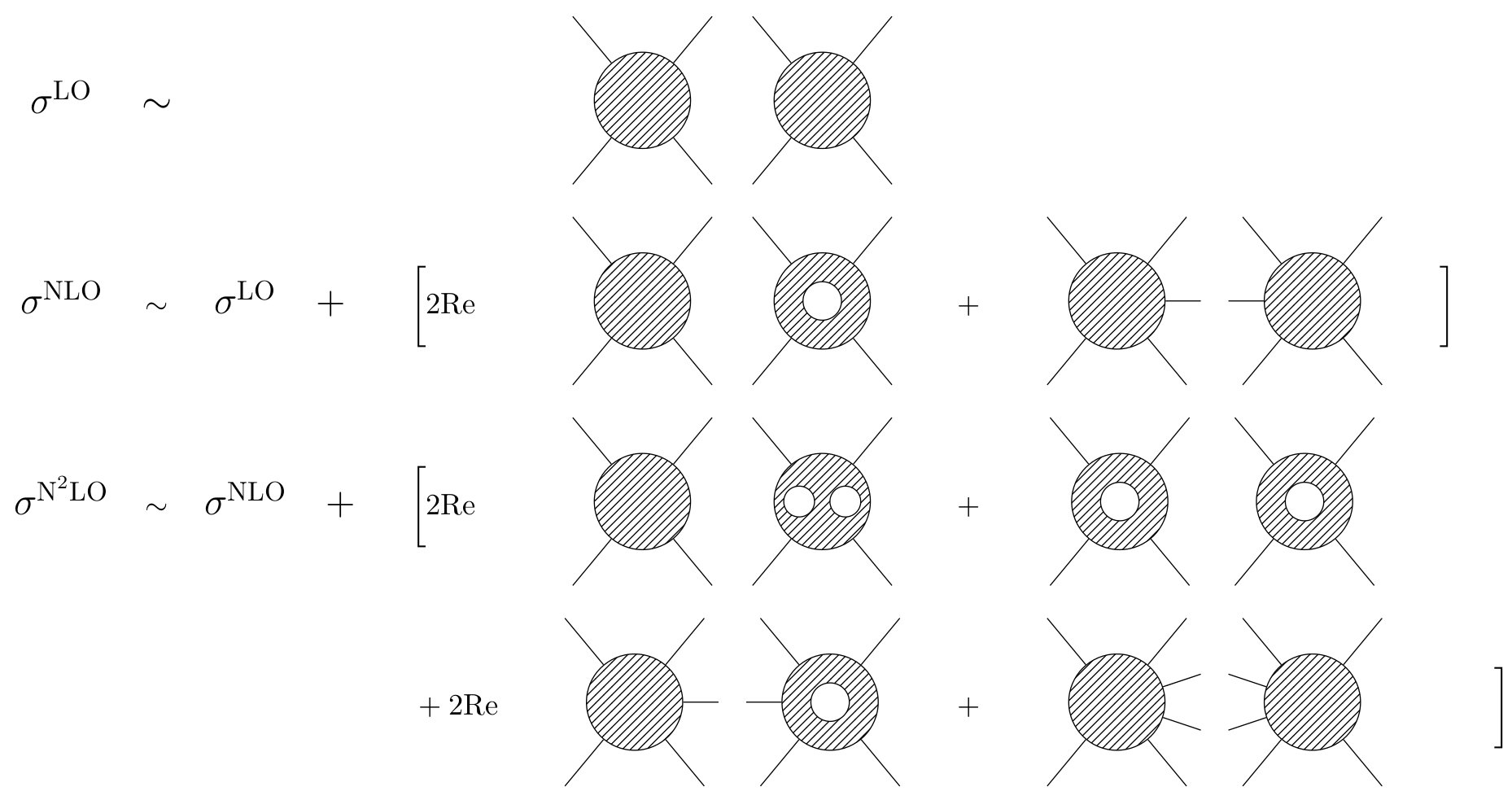
Better predictions require both more loops and higher multiplicity.
| |
|
|||||
| 4 | 5 | 6 | 7 | 8 | ||
| |
0 | |||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
The structure of
Scattering Amplitudes

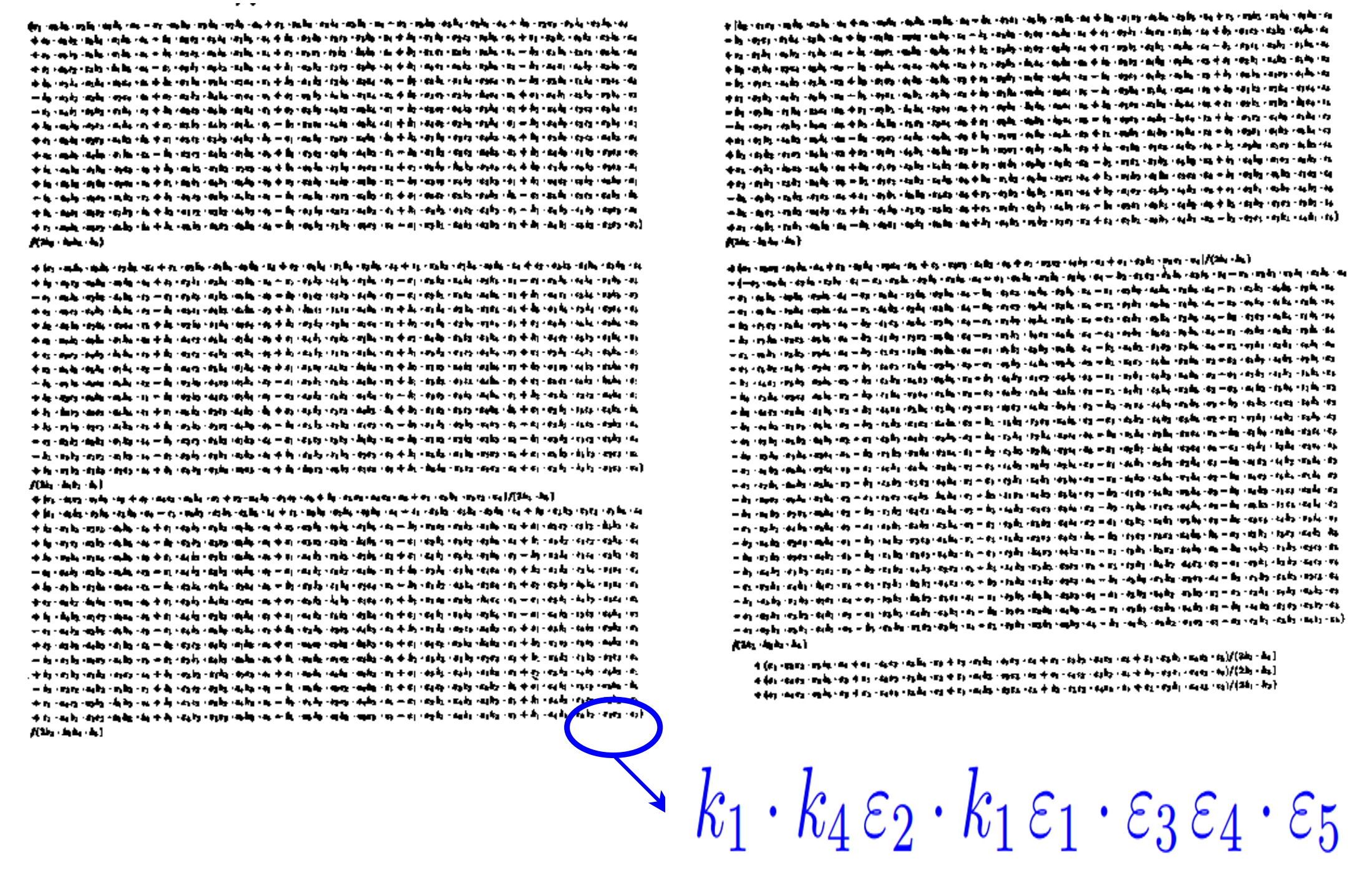
How do we compute Scattering Amplitudes efficiently?
Multi-Loop Amplitudes from Trees
$\circ$ In general, need to solve linear systems for the coefficients $c_{i,\Gamma}$.
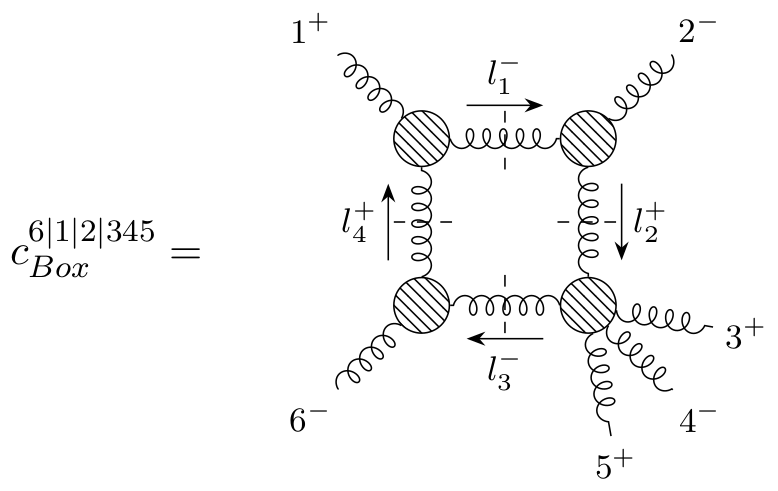
Analytics from Numerics
$\phantom{\circ}\,$ But they are so unstable, even this won't work.
Finite Fields
Analytic Reconstruction
Common-Denominator Ansatz
Tools of the Trade

Perron and Furnon (Google optimization team)
| System Size | Timing |
|---|---|
| 8192 | 8 s |
| 16384 | 51 s |
| 32768 | 6m 30s |
the absolute maximum is 52440 unknowns
(thanks gpu-Merlin!)
Taming the Algebraic Complexity
Its numerator can easily exceed 1 million monomials (e.g. 5-point 1-mass processes).
but how to achieve this without an analytic expression?
The Geometry of Phase Space
based on: GDL, Page (JHEP 12 (2022) 140)
Least Common Denominator Redux
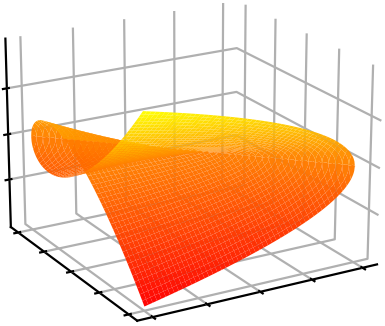
${\color{orange}W_1 = (xy^2 + y^3 - z^2)}$
Multivariate Partial Fractions

${\color{orange}W_1 = (xy^2 + y^3 - z^2)}$

${\color{blue}W_2 = (x^3 + y^3 - z^2)}$
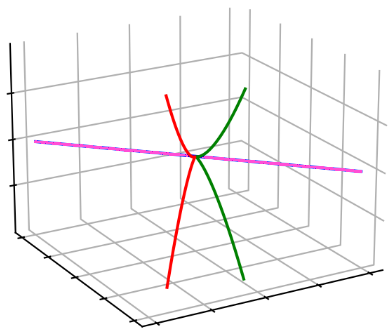
$V(W_1) \cap V(W_2)$
| Kinematics | # Poles ($W$) | LCD Ansatz | Partial-Fraction Ansatz | Rational Functions |
| 5-point massless | 30 | 29k | 4k | $\sim$200 KB |
| Kinematics | # Poles ($W$) | LCD Ansatz | Partial-Fraction Ansatz | Rational Functions |
| 5-point 1-mass | >200 | >5M | $\sim$40k | $\sim$25 MB |
Try it yourself
pip install lips pyadic
Thanks for your attention!
Questions?
Backup Slides
Absolute Values
on the Rationals
$\boldsymbol p\,$-adic Numbers
Python Packages
pyAdic
Related algorithms, such as rational reconstruction are also implemented.
from pyadic import ModP
from fractions import Fraction as Q
ModP(Q(7, 13), 2147483647)
<<< 1817101548 % 2147483647
# Can also go back to rationals
from pyadic.finite_field import rationalise
rationalise(ModP(Q(7, 13), 2147483647))
<<< Fraction(7, 13)
Lips
from lips import Particles
from lips.fields.field import Field
# Random finite field phase space point, arbitrary multiplicity
multiplicity = 5
PSP = Particles(multiplicity, field=Field("finite field", 2 ** 31 - 1, 1), seed=0)
# Evaluate an arbitrary complicated expression
PSP("(8/3s23⟨24⟩[34])/(⟨15⟩⟨34⟩⟨45⟩⟨4|1+5|4])")
<<< 683666045 % 2147483647
Spinor Helicity
Representations of the Lorentz group
(Recall: $\mathfrak{so}(1, 3)_\mathbb{C} \sim \mathfrak{su}(2) \times \mathfrak{su}(2)$)| $(j_{-},j_{+})$ | dim. | name | quantum field | kinematic variable |
|---|---|---|---|---|
| (0,0) | 1 | scalar | $h$ | m |
| (0,1/2) | 2 | right-handed Weyl spinor | $\chi_{R\,\alpha}$ | $\lambda_\alpha$ |
| (1/2,0) | 2 | left-handed Weyl spinor | $\chi_L^{\,\dot\alpha}$ | $\bar{\lambda}^{\dot\alpha}$ |
| (1/2,1/2) | 4 | rank-two spinor/four vector | $A^\mu/A^{\dot\alpha\alpha}$ | $P^\mu/P^{\dot\alpha\alpha}$ |
| (1/2,0)$\oplus$(0,1/2) | 4 | bispinor (Dirac spinor) | $\Psi$ | $u, v$ |
Spinor Covariants
Weyl spinors are sufficient for massless particles:
$\text{det}(P^{\dot\alpha\alpha})=m^2 \rightarrow 0 \quad \Longrightarrow \quad P^{\dot\alpha\alpha} = \bar\lambda^{\dot\alpha}\lambda^\alpha$.In terms of 4-momentum components we have:
$$ \lambda\_\alpha=\frac{1}{\sqrt{p^0+p^3}}\begin{pmatrix}p^0+p^3 \\\ p^1+ip^2\end{pmatrix} \, , \;\;\; \lambda^\alpha=\epsilon^{\alpha\beta} \lambda_\beta =\frac{1}{\sqrt{p^0+p^3}}\begin{pmatrix}p^1+ip^2 \\\ -p^0+p^3\end{pmatrix} $$ $\bar\lambda\_{\dot\alpha}=\frac{1}{\sqrt{p^0+p^3}}\begin{pmatrix}p^0+p^3 \\\ p^1-ip^2\end{pmatrix} \, , \;\;\; \bar\lambda^{\dot\alpha}=\epsilon^{\dot\alpha\dot\beta}\bar\lambda_{\dot\beta}=\frac{1}{\sqrt{p^0+p^3}}\begin{pmatrix}p^1-ip^2 \\\ \-p^0+p^3\end{pmatrix}$$$ \bar\lambda\_{\dot\alpha} = (\lambda\_\alpha)^* \quad if \quad p^i \in \mathbb{R}; \quad \quad \bar\lambda\_{\dot\alpha} \neq (\lambda\_\alpha)^* \quad if \quad p^i \in \mathbb{C} $$
Spinor Invariants
Five-Parton Two-Loop
Finite Remainders
Example Simplifications
uubggg pmpmp Nf1 #3
 is equal to
$
-\frac{[32]^3 [41]^3}{2 [31]^3 [42]^3}
$
is equal to
$
-\frac{[32]^3 [41]^3}{2 [31]^3 [42]^3}
$
ggggg mpmpp Nf1 # 9

is equal to
$-1\frac{[12]³[15][23]⟨25⟩³[35]³}{[13]⁴[25]⟨5|1+2|5]³}+\frac{97}{12}\frac{[12]⁴⟨25⟩[35]⁴}{[13]⁴[25]³⟨5|1+2|5]}$ $+\frac{13}{3}\frac{[12]⁴⟨15⟩[15][35]⁴}{[13]⁴[25]⁴⟨5|1+2|5]}+\frac{1}{4}\frac{[12]⁴⟨15⟩[15]⟨25⟩[35]⁴}{[13]⁴[25]³⟨5|1+2|5]²}$ $-\frac{3}{2}\frac{[12]²⟨25⟩²[25][35]²}{[13]²[25]⟨5|1+2|5]²}+\frac{7}{4}\frac{[12]³⟨25⟩²[35]³}{[13]³[25]⟨5|1+2|5]²}$ $-\frac{43}{3}\frac{[12]³⟨25⟩[35]³}{[13]³[25]²⟨5|1+2|5]}$ $-\frac{25}{3}\frac{[12]³⟨15⟩[15][35]³}{[13]³[25]³⟨5|1+2|5]}$ $-\frac{3}{2}\frac{[12]⟨25⟩[25][35]}{[13][25]⟨5|1+2|5]}$ $+4\frac{[12]²⟨25⟩[35]²}{[13]²[25]⟨5|1+2|5]}$ $-\frac{15}{2}\frac{[12]²[35]²}{[13]²[25]²}$ $+\frac{7}{2}\frac{[12][35]}{[13][25]}$ $-\frac{2}{3}$
Higgs + 4-Parton Amplitude
(@ finite top-mass)
Example of cut diagram
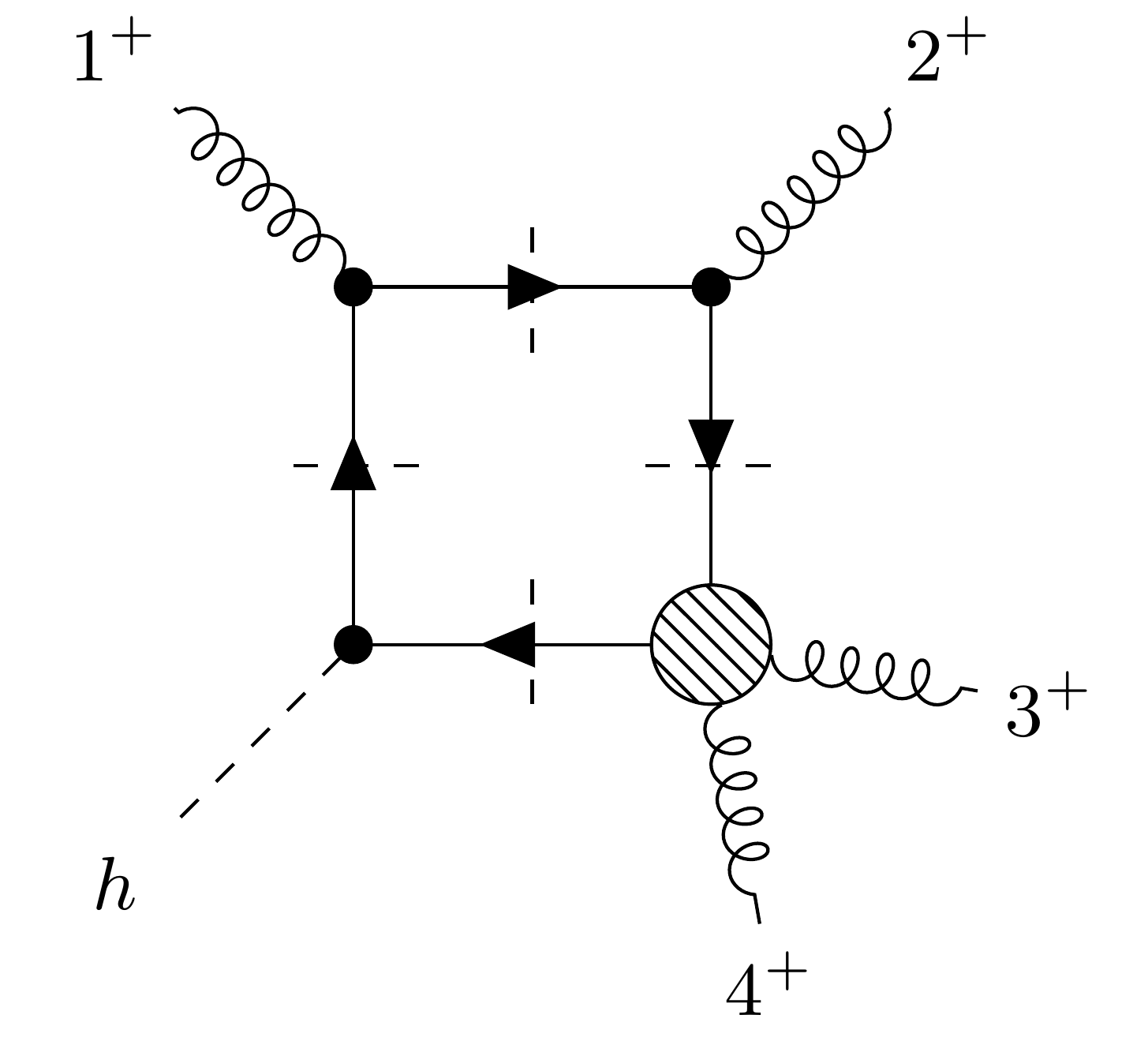
Only singularity involving $m_{top}$ (from pentagon contributions)
$16 |S_{1×2×3×4}| = −s_{12} , s_{23} , s_{34} , \langle 1 |2 + 3|4] , \langle 4|2 + 3|1] + m^2_{top} , tr_5(1234)^2$
We can generate point near this singularity in a similar fashion.
Structure of the coefficients
The massive external leg (the Higgs) is easily accomodated by considering it as a pair of massless particles (think decay products).
In the end all dependance on $P_{Higgs}$ is removed by using momentum conservation.
The coefficients are Taylor expasions in $m_{top}$:
$C^{(0)} + m^2_{top} C^{(2)}$.
with $C^{(0)}$ and $C^{(2)}$ resabling the six-gluon coefficients.