Non-Planar Two-Loop Amplitudes
for Five-Parton Scattering

Giuseppe De Laurentis
University of Edinburgh

arXiv:2311.10086
(GDL, H. Ita, M. Klinkert, V. Sotnikov)
arXiv:2311.18752
(GDL, H. Ita, V. Sotnikov)

Liverpool HEP Seminar



Find these slides at gdelaurentis.github.io/slides/fivepartons_dec2023

Introduction

Cross Sections

Motivations
$\circ$ tri-jet @ $\text{NNLO}$;

$\circ$ di-jet @ $\text{N}^3\text{LO}$;

$\circ$ $\alpha_s$ extraction;

$\circ$ collinear factorization breaking (?);

$\circ$ multi-Regge kinematic limit;

$\circ \; \dots$

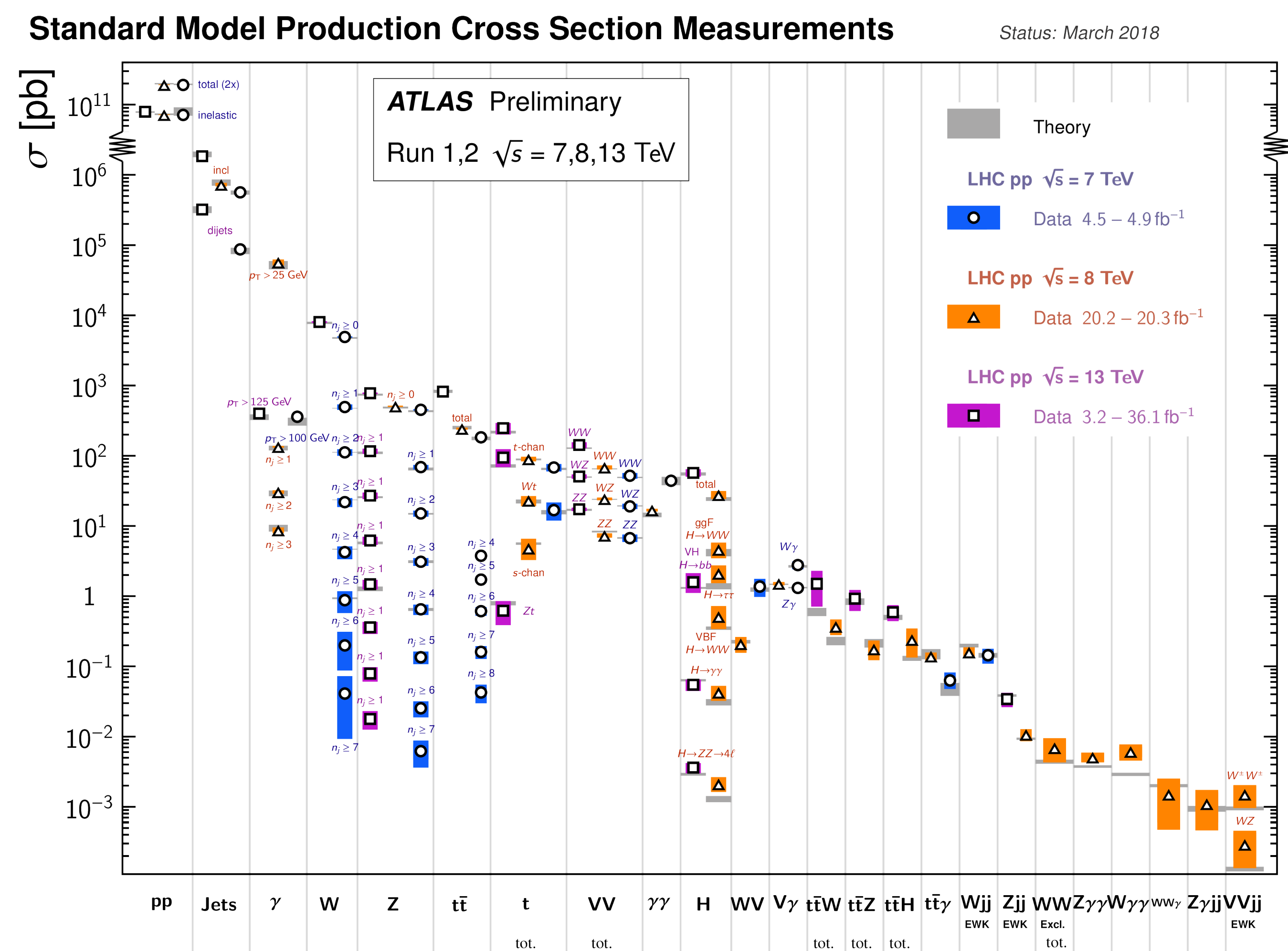
ATLAS Cross-Sections Summary










$$ σ_{2 \rightarrow n - 2} = \sum_{a,b} \int dx_a dx_b f_{a/h_1}(x_a, \mu_F) \, f_{b/h_2}(x_b, \mu_F) \;\hat{\sigma}_{ab\rightarrow n-2}(x_a, x_b, \mu_F, \mu_R) $$
$$ \hat{σ}_{n}=\frac{1}{2\hat{s}}\int d\Pi_{n-2}\;(2π)^4δ^4\big(\sum_{i=1}^n p_i\big)\;|\overline{\mathcal{A}(p_i,h_i,a_i,μ_F, μ_R)}|^2 $$

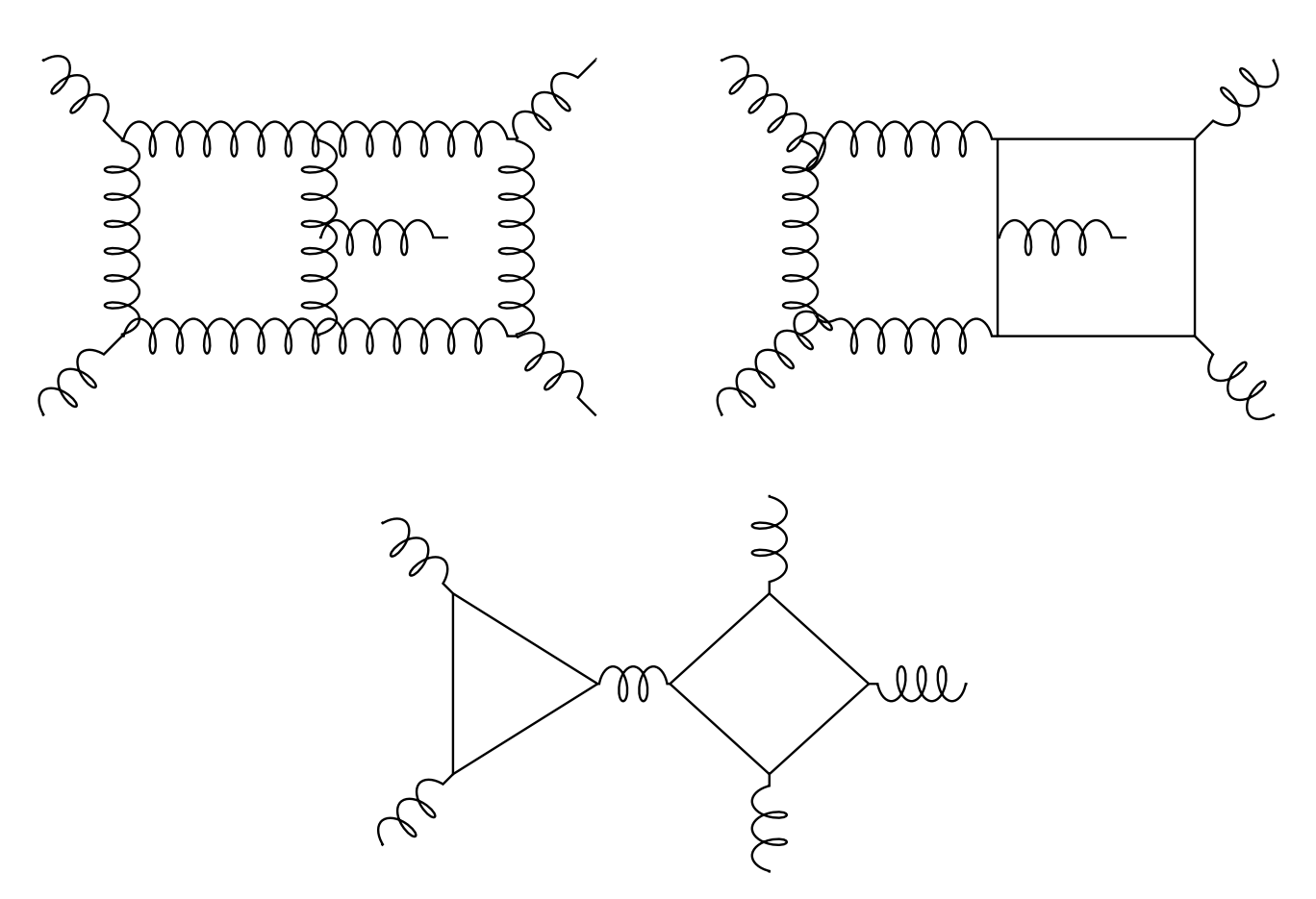
Color Decompositions: ‘‘Trace’’ Basis

\[ \require{color} \require{amsmath} \hspace{-5mm} \begin{align} \mathcal{A}_{\vec{a}}(1_g,2_g,3_g,4_g,5_g) & = \sum_{\sigma \in \mathcal{S}_5/\mathcal{Z}_5} \sigma\Big(\text{tr}(T^{a_1}T^{a_2}T^{a_3}T^{a_4}T^{a_5}) \; A_{1}(1,2,3,4,5)\Big) \; + \\[2mm] & \quad \sum_{\sigma\in \frac{\mathcal{S}_5}{\mathcal{Z}_2 \times \mathcal{Z}_3}} \sigma\Big(\text{tr}(T^{a_1}T^{a_2}) \text{tr}(T^{a_3}T^{a_4}T^{a_5}) \; A_{2}(1,2,3,4,5)\Big) + , \\[8mm] \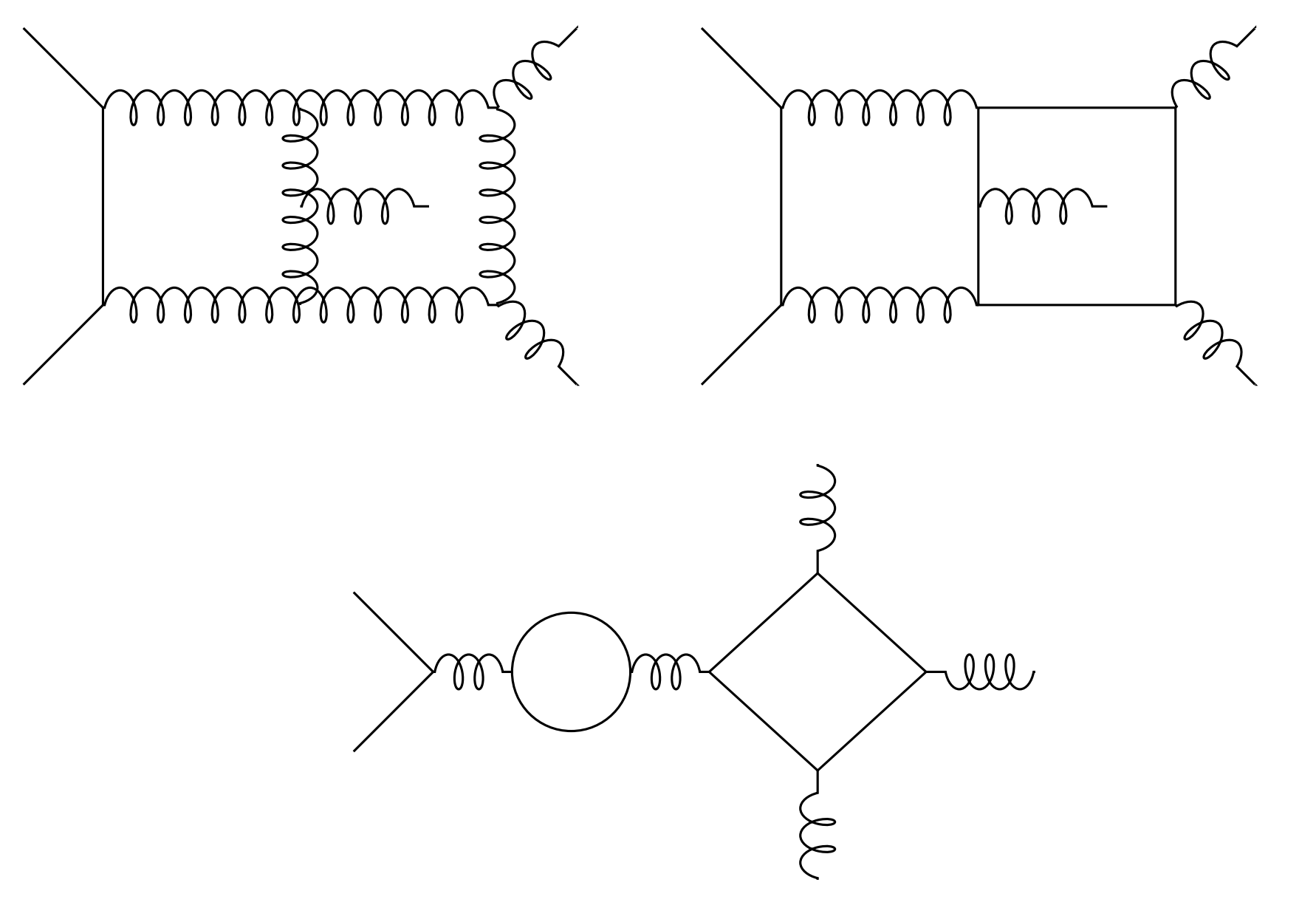mathcal{A}_{\vec{a}}(1_u,2_{\bar u},3_g,4_g,5_g) & = \sum_{\sigma \in \mathcal{S}_3(3,4,5)} \sigma\Big( (T^{a_3}T^{a_4}T^{a_5})^{\,\bar i_2}_{i_1} \; A_{3}(1,2,3,4,5)\Big) \; + \\[2mm] & \quad \sum_{\sigma \in \frac{\mathcal{S}_3(3,4,5)}{\mathcal{Z}_2(3,4)}} \sigma\Big(\text{tr}(T^{a_3}T^{a_4}) (T^{a_5})^{\,\bar i_2}_{i_1} \; A_{4}(1,2,3,4,5)\Big) \; + \\[2mm] & \quad \sum_{\sigma \in \frac{\mathcal{S}_3(3,4,5)}{\mathcal{Z}_{3}(3,4,5)}} \sigma\Big(\text{tr}(T^{a_3}T^{a_4}T^{a_5}) \delta^{\bar i_2}_{i_1} A_{5}(1,2,3,4,5)\Big) \; , \\[8mm] \mathcal{A}_{\vec{a}}(1_u,2_{\bar u},3_d,4_{\bar d},5_g) &= \sum_{\sigma \in \mathcal{Z}_2(\{1,2\},\{3,4\})} \sigma\Big( \delta^{\bar i_4}_{i_1} (T^{a_5})^{\,\bar i_2}_{i_3} \; A_{6}(1,2,3,4,5)\Big) \; + \\[2mm] & \quad \sum_{\sigma \in \mathcal{Z}_2(\{1,2\},\{3,4\})} \kern-2mm \sigma\Big( \delta^{\bar i_2}_{i_1} (T^{a_5})^{\,\bar i_4}_{i_3} \; A_{7}(1,2,3,4,5)\Big)\,,\kern-1mm \end{align} \]
















Each $A_{i}$ has an expansion in powers of $\alpha_s$. We consider the $\alpha_s^2$ corrections.

Color Decompositions: $N_c^{n_c}N_f^{n_f}$ Expansion

Notation = $A_{\scriptscriptstyle \#}^{(L),(n_c, n_f)}$; $\quad$ Red = New; $\quad$ leading color: $n_c + n_f = L$

\[ \begin{gather} \sim\sim\sim\sim 5g \sim\sim\sim\sim\sim \end{gather} \]
\[ \begin{gather} A_1^{(0)} = A^{(0),(0,0)} \, , \quad A_2^{(0)} = 0 \, , \qquad A_1^{(1)} = N_c A^{(1),(1,0)} + N_f A^{(1),(0,1)} \, , \quad A_2^{(1)} = A^{(1),(0,0)} \,, \\[3mm] A_1^{(2)} = N_c^2~A_1^{(2),(2,0)} ~+~ {\color{red} {A_1^{(2),(0,0)}}} + N_c N_fA_1^{(2),(1,1)} + N_c^{-1}N_f ~ {\color{red} {A_1^{(2),(-1,1)}}} + N_f^2 A_1^{(2),(0,2)} \,, \\[3mm] A_2^{(2)} = N_c {\color{red} {A_2^{(2),(1,0)}}} +~ N_f {\color{red} {A_2^{(2),(0,1)}}} ~+~ N_c^{-1}N_f^2 {\color{red} {A_2^{(2),(-1,2)}} }\,. \end{gather} \]
\[ \begin{gather} \sim\sim\sim\sim 2q3g \sim\sim\sim\sim\sim \end{gather} \]
\[ \hspace{-10mm} \begin{gather} A_3^{(0)} = A_3^{(0),(0,0)} \,, \quad A_4^{(0)} = 0\,, \quad A_5^{(0)} = 0\,, \\[4mm] A_3^{(1)} = N_c~A_3^{(1),(1,0)} + N_c^{-1} A_3^{(1),(-1,0)} +N_f A_3^{(1),(0,1)}\,, \quad A_4^{(1)} = A_4^{(1),(0,0)} +N_c^{-1}N_f A_4^{(1),(-1,1)} \,, \quad A_5^{(1)} = A_5^{(1),(0,0)} + N_c^{-1}N_f A_5^{(1),(-1,1)}\,, \\[4mm] A_3^{(2)} = N_c^2~A_3^{(2),(2,0)}+{\color{red} A_3^{(2),(0,0)}}+N_c^{-2} {\color{red} A_3^{(2),(-2,0)}} + N_f N_c~A_3^{(2),(1,1)} + N_c^{-1} {\color{red} A_3^{(2),(-1,1)}} + N_f^2~A_3^{(2),(0,2)}\,, \\[4mm] A_4^{(2)} = N_c~{\color{red} A_4^{(2),(1,0)}} + N_c^{-1} {\color{red} A_4^{(2),(-1,0)}} + N_f{\color{red} A_4^{(2),(0,1)}} + N_c^{-2}N_f {\color{red} A_4^{(2),(-2,1)}} + N_c^{-1}N_f^2 {\color{red} A_4^{(2),(-1,2)}} \\[4mm] A_5^{(2)} = N_c {\color{red} A_5^{(2),(1,0)}} + N_c^{-1} {\color{red} A_5^{(2),(-1,0)}} + N_f N_c{\color{red} A_5^{(2),(1,1)}} + N_c^{-2}N_f {\color{red} A_5^{(2),(-2,1)}} + N_c^{-1}N_f^2 {\color{red} A_5^{(2),(-1,2)}} \,. \end{gather} \]
Relations among Partials
\[ \begin{gather} \sim\sim\sim\sim \text{Known relations for } 5g \sim\sim\sim\sim\sim \end{gather} \]
\[ \begin{gather} A_1^{(2),(0,0)} = \sum_\sigma c_\sigma A_1^{(2),(2,0)}(\sigma_1,\dots,\sigma_5) + \sum_\sigma c_\sigma A_2^{(2),(1,0)}(\sigma_1,\dots,\sigma_5) \qquad \text{(schematically)} \end{gather} \]
\[ \begin{gather} \sim\sim\sim\sim 4q1g \text{ expansion} \sim\sim\sim\sim\sim \end{gather} \]
\[ \begin{gather} A_6^{(0)} = A_6^{(0),(0,0)} \,, \quad A_7^{(0)} = \frac{1}{N_c} A_7^{(0),(-1,0)} \,, \\ A_6^{(1)} = N_c A_6^{(1),(1,0)} + \frac{1}{N_c} A_6^{(1),(-1,0)} + N_f A_6^{(1),(0,1)} \,,\quad A_7^{(1)} = A_7^{(1),(0,0)} + \frac{1}{N_c^2} A_7^{(1),(-2,0)} + \frac{N_f}{N_c} A_7^{(1),(-1,1)} \,, \\[2mm] A_6^{(2)} = N_c^2 A_6^{(2),(2,0)} + {\color{red} A_6^{(2),(0,0)}} + \frac{1}{N_c^2} {\color{red} A_6^{(2),(-2,0)}} + N_f N_c A_6^{(2),(1,1)} + \frac{N_f}{N_c} {\color{red} A_6^{(2),(-1,1)}} + N_f^2 A_6^{(2),(0,2)} \\ A_7^{(2)} = N_c {\color{red} A_7^{(2),(1,0)}}+\frac{1}{N_c}{\color{red} A_7^{(2),(-1,0)}}+\frac{1}{N_c^3}{\color{red} A_7^{(2),(-3,0)}} + N_f{\color{red} A_7^{(2),(0,1)}} + \frac{N_f}{N_c^2} {\color{red} A_7^{(2),(-2,1)}} + \frac{N_f^2}{N_c}{\color{red} A_7^{(2),(-1,2)}}\,. \end{gather} \]
\[ \begin{gather} \sim\sim\sim\sim \text{New relations for } 4q1g \text{ (technically for the remainders)} \sim\sim\sim\sim\sim \end{gather} \]
\[ \Big\{ \big[ 16 \, A^{(2),(2,0)}_6\, (1,2,3,4,5) + 4 \, A^{(2),(0,0)}_6\, (1,2,3,4,5) + A^{(2),(-2,0)}_6(1,2,3,4,5) \big] - \big[\dots \big]_{3 \leftrightarrow 4} \Big\} - \Big\{ \dots \Big\}_{1 \leftrightarrow 2} = 0 \, . \]
\[ \begin{gather} \big[ 32 \, A^{(2),(2,0)}_6\, (1,2,3,4,5) + 8 \, A^{(2),(0,0)}_6\, (1,2,3,4,5) + 2 A^{(2),(-2,0)}_6(1,2,3,4,5) \\ + 16 \, A^{(2),(1,0)}_7\, (1,2,3,4,5) \, + 4 A^{(2),(-1,0)}_7(1,2,3,4,5) + A^{(2),(-3,0)}_7 (1,2,3,4,5) \big] - \big[ \dots \big]_{3 \leftrightarrow 4}= 0 \, . \end{gather} \]
Plus two more for the $N_f^1$ partials.
Number of Cut Diagrams

Partial Amplitudes

$\circ$ Amplitude (integrands) can be written as (drop the extra sub- and super-scripts)

$$ \displaystyle A(\lambda, \tilde\lambda, \ell) = \sum_{\substack{\Gamma,\\ i \in M_\Gamma \cup S_\Gamma}} \, c_{\,\Gamma,i}(\lambda, \tilde\lambda, \epsilon) \, \frac{m_{\Gamma,i}(\lambda\tilde\lambda, \ell)}{\textstyle \prod_{j} \rho_{\,\Gamma,j}(\lambda\tilde\lambda, \ell)} \;\; \xrightarrow[]{\int d^D\ell} \;\; \sum_{\substack{\Gamma,\\ i \in M_\Gamma}} {\color{red}c_{\,\Gamma, i}}(\lambda, \tilde\lambda, \epsilon) \, {\color{orange}I_{\Gamma, i}}(\lambda\tilde\lambda, \epsilon) $$

$\circ$ For a suitable choice of integrands, we get:

$$ \displaystyle {\color{red}c_{\Gamma, i}}(\lambda, \tilde\lambda, \epsilon) = \frac{ \sum_{k=0}^{\text{finite}} \, {\color{red}c^{(k)}_{\,\Gamma, i}}(\lambda, \tilde\lambda) \, \epsilon^k}{\prod_j (\epsilon - a_{ij})} \;, \;\;\text{with} \quad a_{ij} \in \mathbb{Q} \, . $$

Some notation:

$\circ$ $\Gamma$: topologies $\quad\circ$ $M_\Gamma$: master integrands $\quad\circ$ $S_\Gamma$: surface terms $\quad\circ$ $D = 4 - 2 \epsilon$
$\circ$ Spinors: $\lambda_i = |i\rangle, \tilde\lambda_i =[i|$ $\quad\circ$ External 4-momenta: $\lambda\tilde\lambda=p\kern-3mm/$ $\quad\circ$ Loop $D$-momenta: $\ell $

Numerical Computation

Numerical Generalized Unitarity
Ita (‘15) Abreu, Febres Cordero, Ita, Page, Zeng (‘17)

$\circ$ We have an Ansatz for the loop integrand

$$ \require{color} \displaystyle A(\lambda, \tilde\lambda, \ell) = \sum_{\Gamma} \, \sum_{i \in M_\Gamma \cup S_\Gamma} \, c_{\,\Gamma,i}(\lambda, \tilde\lambda) \, \frac{m_{\Gamma,i}(\lambda\tilde\lambda, \ell)}{\textstyle \prod_{j} \rho_{\,\Gamma,j}(\lambda\tilde\lambda, \ell)} $$
$\circ$ Generalized unitarity relates cuts of loop amplitudes to products of trees
$$ \require{color} \displaystyle \sum_{\text{states}} \, \prod_{\text{trees}} A^{\text{tree}}(\lambda, \tilde\lambda, \ell)\big|_{\text{cut}_{\Gamma}} = \sum_{\substack{\Gamma' \ge \Gamma, \\ i \in M_\Gamma' \cup S_\Gamma'}} \kern-2mm c_{\,\Gamma',i}(\lambda, \tilde\lambda) \, \frac{m_{\Gamma',i}(\lambda\tilde\lambda, \ell)}{\displaystyle \prod_{j\in P_{\Gamma'} / P_{\Gamma}} \rho_{j}(\lambda\tilde\lambda, \ell)}\Bigg|_{\text{cut}_\Gamma} $$
Numerical Berends-Giele recursion for LHS, solve for coeffs. in RHS.
Perhaps show Box and Triangle example from my PhD thesis page 63

Integration By Parts Reduction

$\circ$ Master / surface decomposition for non-planar topologies
$$ \require{color} \begin{align} \kern-25mm \text{IBP-generating vectors: } & \quad \displaystyle \int d^D \ell \frac{\partial }{\partial \ell^\mu_a} \frac{v^\mu_a(\ell)}{\rho_1 \dots \rho_N} = 0 \quad (\text{in dim. reg.}) \\[2mm] \kern-25mm \text{No propagator doubling: } & \quad \displaystyle \sum_{a, \mu} v^\mu_a(\ell) \frac{\partial \rho_i}{\partial \ell^\mu_a} - f_i(\ell)\rho_i = 0 \end{align} $$
$(v^\mu_a, f_i)$ form a syzygy module, solved for in embedding space using Singular + linear algebra.
$\circ$ Semi-numerical surface terms: $\quad m_{i\in S_\Gamma}(\ell \leftarrow \text{analytical}, s_{ij} \leftarrow \text{numerical})$
$\kern20mm\star$ dependance on external kinematics ($s_{ij}$) obtained from sparse linear systems.

$\circ$ Little group information retained throughout the computation
$\kern20mm\star$ genuine $c_{\Gamma,i}(\lambda, \tilde\lambda)$ instead of $c_{\Gamma,i}(\lambda\tilde\lambda)$ + conventions for the polarization states.

Finite Remainders

$\circ$ Dim-reg is great, but it also introduces a lot of junk (see next slide).
$\circ$ All physical information is contained in the finite remainder, at two loops
$$ \underbrace{\mathcal{R}^{(2)}}_{\text{finite remainder}} = \mathcal{A}^{(2)}_R \underbrace{- \quad I^{(1)}\mathcal{A}^{(1)}_R \quad - \quad I^{(2)}\mathcal{A}^{(0)}_R}_{\text{divergent + convention-dependent finite part}} + \mathcal{O}(\epsilon) $$
$\phantom{\circ}$ $\mathcal{A}^{(1)}_R$ to order $\epsilon^2$ is still needed to build $\mathcal{R}^{(2)}$, but there is no reason to reconstruct it
Although by the time I learned this, I had already reconstructed $\mathcal{A}^{(1)}_{5g}$ to $\epsilon^2$ $\qquad$

$\circ$ Finite remainder as a weighted sum of pentagon functions Chicherin, Sotnikov ('20); 
$$ \textstyle \mathcal{R}(\lambda, \tilde\lambda) = \sum_i \color{orange}{r_{i}(\lambda,\tilde\lambda)} \, \color{red}{h_i(\lambda\tilde\lambda)} $$
Goal: Reconstruct $\color{orange}{r_{i}(\lambda,\tilde\lambda)}$ from $\mathbb{F}_p$ samples
von Manteuffel, Schabinger ('14)
Peraro ('16)
$\circ$ More precisely, we would like a basis of the vector space $\text{span}(r_i(\lambda,\tilde\lambda))$
$\phantom{\circ}$ (given a basis, obtaining the full set is easy).

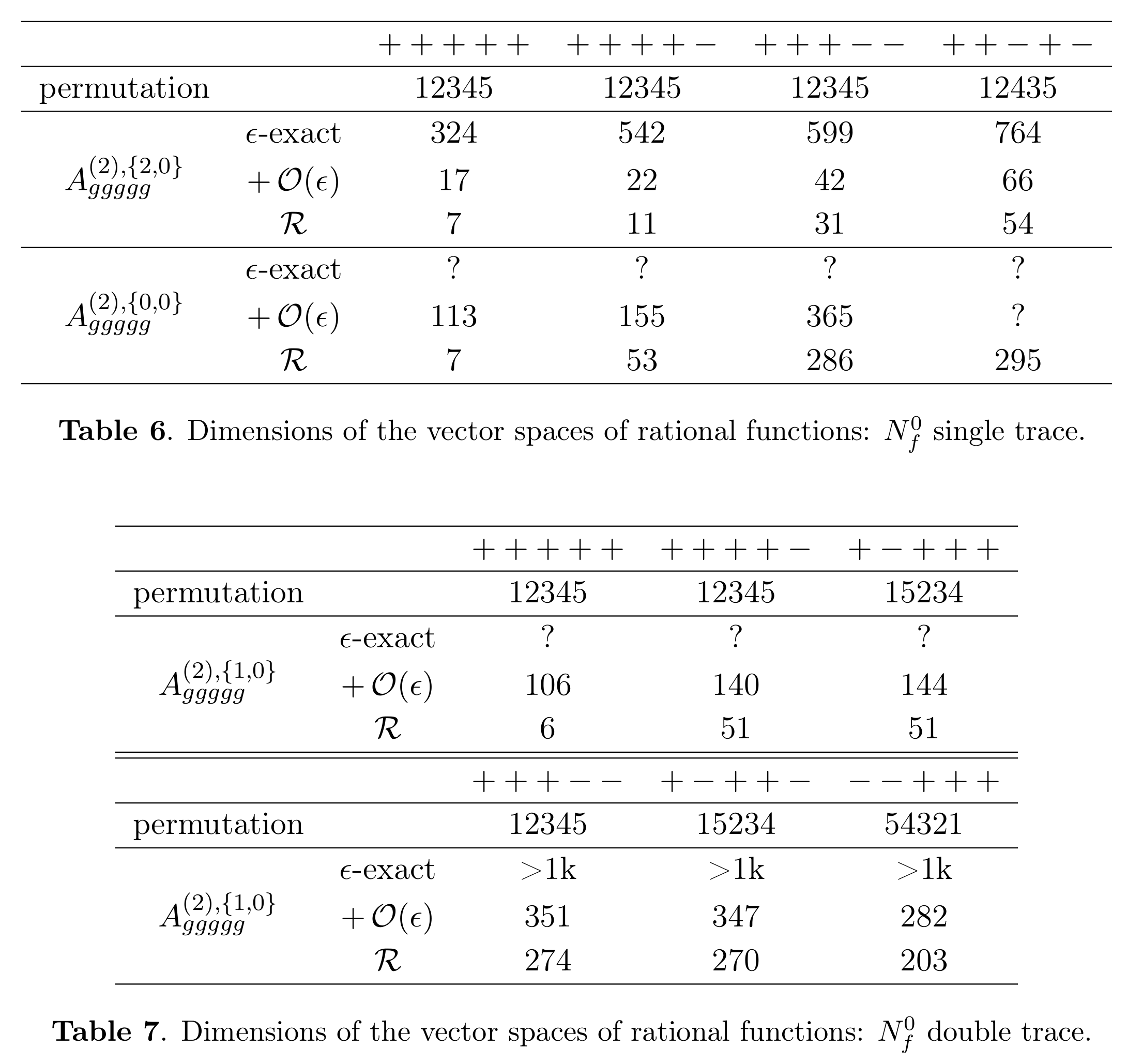
Number of Indep. Functions w/o Subtraction

Technical Interlude: Python Wrapper

$\circ$ Reason 1 : The rational reconstruction, $\mathbb{F}_p \rightarrow \text{Rational Function}$, is much cheaper than numerical evaluations. I want to use Jupyter for interactive analysis and development.
$\circ$ Reason 2 : Evaluations cost up to 1-2 hours, per phase-space point, per partial amplitude! I need up to ~35k points per partial. (Less for the quark channels, see later.)
We better have some caching!
$\circ$ Pseudo-random squences of phase-space points over $\mathbb{F}_p$ or $\mathbb{Q}_p$ generated using lips & pyadic
$\circ$ Custom (for now private) interface to Caravel, key features: $\phantom{\circ}\;$ (for Caravel developers see pynta)
$\quad \star$ caching to a SQLite database using diskcache via Python decorators;
$\quad \star$ distributed computing into a slurm cluster (use_slurm_cluster=True);
$\quad \star$ functions for IR/UV subtraction, CaravelGraph, and PentagonFunctions parsing;
$\quad \star$ permutations of amplitudes w/o changing call to Caravel.





Analytic and Geometric Structure





based on:
GDL, Page (JHEP 12 (2022) 140)
GDL, Ita, Page, Sotnikov (to appear)

Polynomial Quotient Rings

$\circ$ Let us start from the polynomial ring of spinor components

$$\displaystyle \kern-50mm S_n = \mathbb{F}\left[|1⟩, [1|, \dots, |n⟩, [n|\right]$$

$\phantom{\circ}$ the field $\mathbb{F}$ can be any of $\mathbb{Q},\mathbb{R},\mathbb{C},\mathbb{F}_p,\mathbb{Q}_p,\dots$

$\circ$ Define the momentum-conservation ideal as
$$ \displaystyle J_{\Lambda_n} = \Big\langle \sum_i |i⟩[i| \Big\rangle_{S_n} $$

Artist's Impression of $V(J_{\Lambda_n})$
I can't draw in $4n$ dims!

$\phantom{\circ}$ physically, two polynomials $p$ and $q$ are equivalent if $p-q\in J_{\Lambda_n}$

$\circ$ This defines the needed polynomial quotient ring$\kern-4mm\phantom{x}^{\star}$: $\;R_n = S_n / J_{\Lambda_n} $
$r_i(\lambda, \tilde\lambda)$ at $n$-point belong to the Field of Fractions$\kern-4mm\phantom{x}^{\dagger}$ of $R_n$
$\kern-4mm\phantom{x}^\star R_4$ is "weird" (not a UFD), but it proves that polynomial rings are insufficient; $\;\kern-4mm\phantom{x}^\dagger$ The field of fractions of $R_3$ does not exist.

Prime Ideals & Irreducible Varieties

$\circ$ Let us consider a very simple example (at 4-point)

$\displaystyle \kern-50mm iA_{g^-g^-g^+g^+}^{\text{tree}} = \frac{\langle 12 \rangle^3}{\langle 23 \rangle \langle 34 \rangle \langle 41 \rangle} = \frac{[34]^3}{[12][23][41]} $

$\phantom{\circ}$ is, say, $\langle 23 \rangle$ a pole of this amplitude?

Artist's Impression of $V(\big\langle \langle 23 \rangle\big\rangle_{R_4})$
as the union of two irreducibles

$\circ$ The question is ill posed!
$\phantom{\circ} \langle 23 \rangle$ does not identify an irreducible variety in $R_4$.
$\phantom{\circ}$ Compute $\color{green}\text{primary decompositions}$, such as
$\displaystyle \big\langle \langle 23\rangle \big\rangle_{R_4} = {\color{orange} \big\langle \langle 23\rangle, [14] \big\rangle_{R_4}} \cap {\color{blue} \big\langle \langle 12\rangle, \langle 13 \rangle, \langle 14\rangle, \langle 23\rangle, \langle 24 \rangle, \langle 34 \rangle \big\rangle_{R_4}} $

$\phantom{\circ}$ On the first branch there is a simple pole, on the latter branch the amplitude is regular.
Poles & Zeros $\;\Leftrightarrow\;$ Irreducible Varieties $\;\Leftrightarrow\;$ Prime Ideals
Physics $\kern38mm$ Geometry $\kern38mm$ Algebra

Five-Point Kinematics

$\circ\,$ The rational coefficients take the form

$$ \displaystyle r_i(|i\rangle,[i|) = \frac{\text{Num. poly}(|i\rangle,[i|)}{\text{Denom. poly}(|i\rangle,[i|)} = \frac{\mathcal{N}(|i\rangle,[i|)}{\prod_j D_j^{q_{ij}}(|i\rangle,[i|)} $$
$\circ\,$ The denominator factors $\mathcal{D}_j$ are conjectured to be restricted to the letters of the symbol alphabet
Abreu, Dormans, Febres Cordero, Ita, Page ('18)
$$ \displaystyle \{\mathcal{D}_{\{1,\dots,35\}}\} = \bigcup_{\sigma \; \in \; \text{Aut}(R_5)} \sigma \circ \big\{ \langle 12 \rangle, \langle 1|2+3|1] \big\} \, , \qquad \text{Aut}(R_5) = \mathcal{P} \times \mathcal{S}_5 $$
$\qquad\color{green}\text{Identical to 1-loop!}$
$\phantom{\circ}$ Non-trivial statement (not proven!): all irreducible polynomials generate prime ideals, @ 5-pt.

$\circ\,$ Advantage of spinor variables:

$1.$ little group covariant LCD (no spurious poles); $\;\;2.$ avoiding parity even/odd split.
$\Rightarrow\;$ fewer and simpler functions to reconstruct compared to Mandelstams or Twistors.
Next we obtain the denomiantor exponents $q_{ij}$.

Least Common Denominator

$\circ\,$ The exponents $q_{ij}$ are given by

$$ \displaystyle \lim_{\mathcal{D}_j \rightarrow 0} r_i = (\mathcal{O}(1) \text{ const.}) \times \mathcal{D}_j^{-q_{ij}} $$
$\circ\,$ Issue: this can be done for $\mathbb{R}$, $\mathbb{C}$, $\mathbb{Q}_p$ but not $\mathbb{F}_p$ .
$\circ\,$ Solution: univariate Thiele rational interpolation on a line going through $V(\langle \mathcal{D}_j \rangle)$

$$ \displaystyle |i\rangle \rightarrow |i\rangle (t) = |i\rangle + t c_i |\eta\rangle , \qquad |i] \rightarrow |i] \, , \qquad \text{s.t.} \quad \sum_i c_i |i] = 0 $$
$\circ\,$ After interpolation on the (anti-)holomorphic slice, the rational functions read

$$ \displaystyle r_i(t) = \frac{\text{Poly. }(t)}{\prod_j (t-t_{\mathcal{D}_j})^{q_{ij}}} $$
where $t_{\mathcal{D}_j}$ is simply the solution to $D_j(t) = 0$. We read off the $q_{ij}$.

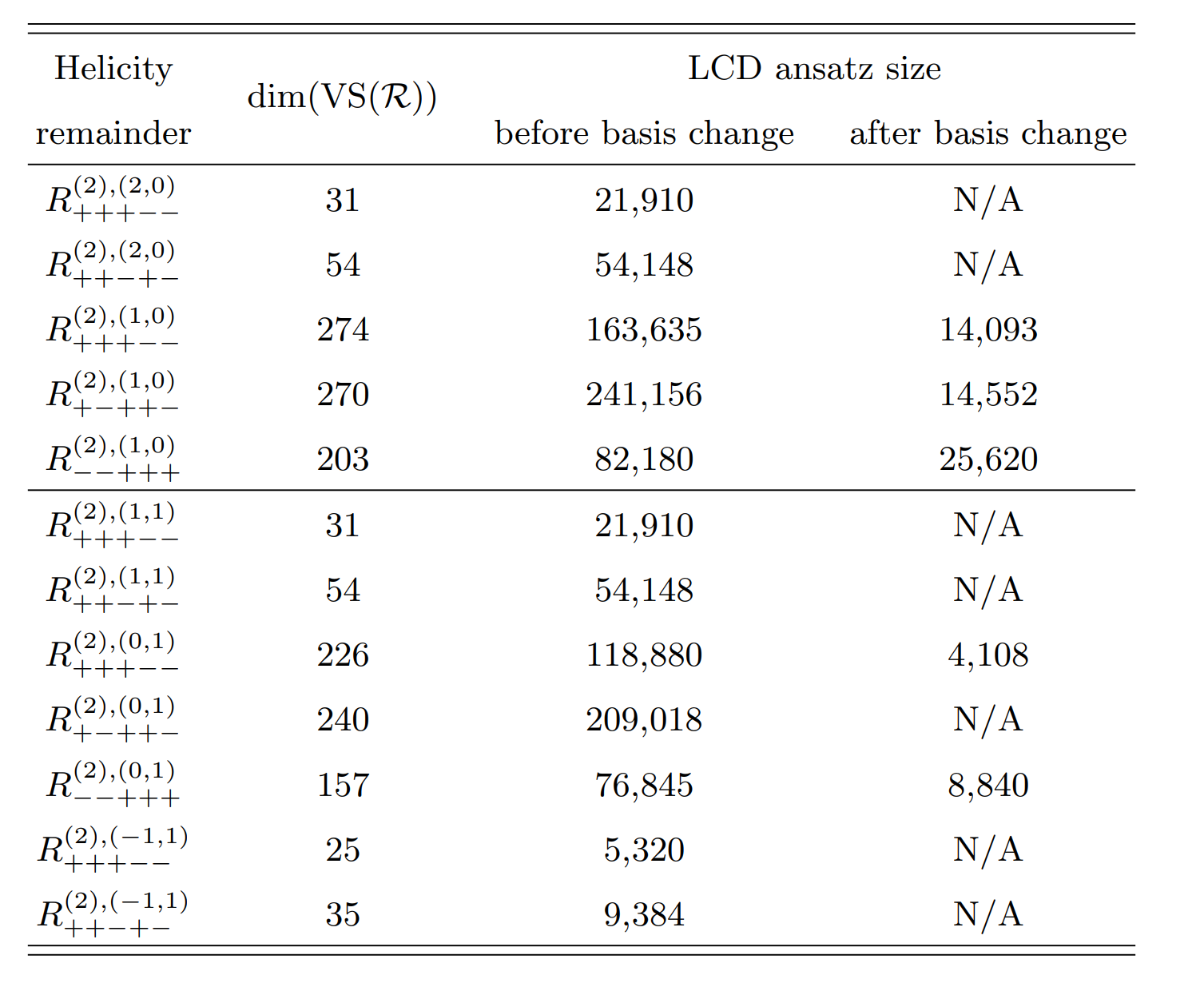
Complexity of the Reconstruction

$\circ\,$ Sort the $r_i$ by mass dimension of $\mathcal{N}$ ($\approx$ Ansatz size), pick simplest subset forming a basis $r_{i \in \mathcal{B}}$

Analytic Reconstruction

Picking a Basis

$\circ\,$ We currently have:

$$ R = r_{i\in \mathcal{B}} M_{ij} h_j \, , \qquad M_{ij} \in \mathbb{Q} $$
$\phantom{\circ}\,$ with $r_{i\in \mathcal{B}} \subset r_i$, i.e. $M_{ij}$ is in reduced row echelon form, up to a permutation of columns.
$\circ\,$ Basic idea: change basis from a subset of pentagon function coefficients, to linear combinations


$$ \tilde{r}_{i'} = O_{i'i} \, r_{i \in \mathcal{B}} \quad \text{s.t.} \quad \text{rank}(O_{i'i}) = \text{dim(span}_{FF(R_5), \mathbb{Q}}(r_{i})) $$
$\circ\,$ Key insight:

$$ \text{dim(span}_{FF(R_5), \mathbb{Q}}\left(\lim_{\mathcal{D_j} \rightarrow 0 }r_{i}\right)) \leq \text{dim(span}_{FF(R_5), \mathbb{Q}}(r_{i})) $$
$\phantom{\circ}\,$ I.e., the pole residues are correlated, build linear combinations that ''remove the overlap''

Correlation of Residues

$\circ\,$ Build Laurent expansions around $t_{\mathcal{D}_k}$ (use same kind of slice as before)

$$ r_{i \in \mathcal{B}} = \sum_{m = 1}^{q_k = \text{max}_i(q_{ik})} \frac{e^k_{im}}{(t-t_{\mathcal{D}_k})^m} + \mathcal{O}((t-t_{\mathcal{D}_k})^0) $$
$\phantom{\circ}\,$ strictly formal over $\mathbb{F}_p$, but convergent over $\mathbb{Q}_p$ for $(t-t_{\mathcal{D}_k}) \propto p$
$\circ\,$ Repeat for several (anti-)holomorphic slices, build vectors


$$ \vec{e}^k_{im} = (e^k_m)_{ij} = \{ e^k_{im}(\text{slice}_1), \dots, e^k_{im}(\text{slice}_n) \} $$
$\circ\,$ By Gaussian elimination on the matrix $(e^k_m)_{ij}$ we can partition the space:

$$ \text{span}_{\vec{\mathbb{Q}},\mathbb{Q}}(r_{i \in \mathcal{B}}) = \text{column}_{\vec{\mathbb{Q}},\mathbb{Q}}(\text{Res}(r_{i \in \mathcal{B}}, D_k^m)) \oplus \text{null}_{\vec{\mathbb{Q}},\mathbb{Q}}(\text{Res}(r_{i \in \mathcal{B}}, D_k^m)) $$
Interpretation of $\text{null}_{\vec{\mathbb{Q}},\mathbb{Q}}(\text{Res}(r_{i \in \mathcal{B}}, D_k^m)) \cdot r_{i \in \mathcal{B}}$: functions that do not have a $D_k^m$ singularity

Breadth-First Search

$\circ\,$ If a function $\tilde{r}$ does not have poles $D_{k_1}^{m_1}$ and $D_{k_2}^{m_2}$, then

$$ \tilde{r} \in \text{span}_{FF(R_5),\mathbb{Q}}\Bigg[\Big(\text{null}_{\vec{\mathbb{Q}},\mathbb{Q}}(\text{Res}(r_{i \in \mathcal{B}}, D_{k_1}^{m_1})) \cap \text{null}_{\vec{\mathbb{Q}},\mathbb{Q}}(\text{Res}(r_{i \in \mathcal{B}}, D_{k_2}^{m_2}))\Big)_{i'i} \; \cdot \; r_{i\in \mathcal{B}}\Bigg] $$
$\circ\,$ Build linear combination that remove as many singularities as possible, without dropping rank

$$ \displaystyle O_{i'i} = \cap_{k, m} \, \text{nulls}_{\vec{\mathbb{Q}},\mathbb{Q}} \qquad \text{(schematically)} $$
$\circ\,$ This is done by searching a tree of possibilities of which pole gets dropped to which order.
$\phantom{\circ}\,$ Several optimizations required to search an otherwise proibitively large space, naively of size


$$ \prod_k (m_k + 1) \quad \text{with } \; k \;\text{ enumerating } \; D_k^{m_k} $$

Least Least-Common-Denominator

$\circ$ In other words, we have reshuffled the $r_i$ by linear combinations of the others $r_{j\neq i}$
$\displaystyle \tilde{r}_i = \sum_{j\neq i} O_{ij} r_j + r_i$

$\circ\,$ The rational functions now take the form

$$ \displaystyle \tilde{r}_i(|i\rangle,[i|) = \frac{\tilde{\mathcal{N}}(|i\rangle,[i|)}{\prod_j D_j^{\tilde{q}_{ij}}(|i\rangle,[i|)} $$
$\phantom{\circ}\,$ where we have minimized $\sum_j \tilde{q}_{ij}$, compared to the $r_i$.

$\circ\,$ This is the closest thing that I am aware of to a Gram–Schmidt procedure for vector spaces over fields that are not number fields, but in this case fields of fractions over polynomial quotient rings.
$\circ\,$ Can we think of this as defining an inner product on the space of rational functions?



$$ O_{ij} \sim \langle r_i | r_j \rangle \qquad \text{(very schematically)} $$

The Numerator Ansatz

$\circ\,$ The numerator Ansatz takes the form
GDL, Maître ('19)
$\displaystyle \text{Num. poly}(\lambda, \tilde\lambda) = \sum_{\vec \alpha, \vec \beta} c_{(\vec\alpha,\vec\beta)} \prod_{j=1}^n\prod_{i=1}^{j-1} \langle ij\rangle^{\alpha_{ij}} [ij]^{\beta_{ij}}$
$\phantom{\circ}$ subject to constraints on $\vec\alpha,\vec\beta$ due to: 1) mass dimension; 2) little group; 3) linear independence.

$\circ\,$ Construct the Ansatz via the algorithm from Section 2.2 of GDL, Page ('22)
Linear independence = irreducibility by the Gröbner basis of a specific ideal.
$\circ\,$ Efficient implementation using open-source software only

Gröbner bases $\rightarrow$ constrain $\vec\alpha,\vec\beta$
Decker, Greuel, Pfister, Schönemann

Integer programming $\rightarrow$ enumerate sols. $\vec\alpha,\vec\beta$
Perron and Furnon (Google optimization team)





$\circ\,$ Linear systems solved w/ CUDA over $\mathbb{F}_{2^{31}-1}$ ($t_{\text{solving}} \ll t_{\text{sampling}}$) w/ linac (coming soon-ish)

Spinor-Helicity Results

$\circ$ For the first time with an MHV two-loop five-point amplitude the results for the rational coefficients are compact enough to be present within a paper

https://arxiv.org/pdf/2311.10086.pdf#page=14

$\circ$ The simplification of the basis change is independent of that obtained from partial fraction decompositions, as the latter can still be performed after the former.
$\circ$ Can now study propertities of the amplitude
$\phantom{\circ}$ e.g. no function has a $\text{tr}_5$ singularity, nor a pair of $\langle i | j + k | i]$ in the same denominator.

Quarks from Gluons

$\circ$ Checking whether a rational function belongs to a given vector space
$$ r_{\text{guess}} \stackrel{?}{\in} \text{span}_{FF(R_5), \mathbb{Q}}(r_{i}) $$
$\phantom{\circ}$ is much simpler problem than performing a rational reconstruction!
$\phantom{\circ}$ It only requires as many evaluations as the dimension of the vector space.
$\circ$ The vector space has uniform mass dimension and phase weights
$$ |i⟩ \rightarrow t^{1/2}|i⟩, \; |i] \rightarrow t^{1/2}|i] \quad \forall \; i \quad \text{and} \quad |i⟩ \rightarrow t|i⟩, \; |i] \rightarrow \frac{1}{t}|i] $$
$\circ$ Generate guesses for quark functions by re-scaling gluon functions
$$ \tilde{r}^{-}_{73}(q^+,q^-,g^+,g^+,g^-) = \frac{[14]⟨25⟩⟨45⟩}{⟨24⟩[24]⟨34⟩^2} = \frac{⟨14⟩}{⟨24⟩} \underbrace{\frac{[14]⟨25⟩⟨45⟩}{⟨14⟩[24]⟨34⟩^2}}_{r^{--}_{18}(g^+,g^-,g^+,g^+,g^-)} $$
$\circ$ We obtain most (50% of 2q3g and 90% of 4q1g) quarks functions this way.

Outlook

5-point 1-mass Amplitudes: e.g. Wjj
$0.\,$ Start from analytics of Abreu, Febres Cordero, Ita, Klinkert, Page, Sotnikov ('21) - 1.2GB of C++ source code.
$1.\,$ Script to split up the expressions, and compile them ($\sim 20$GB binaries) for evaluation over $\mathbb{F}_p$;
$2.\,$ Recombine the 3 projections $p_V \parallel p_1, p_V \parallel p_2, p_V \parallel p_3$ and reintroduce the little group factors
to build 6-point spinor-helicity amplitudes (subject to degree bounds on $|5\rangle,[5|,|6\rangle,[6|$);
$3.\,$ Perform (rough) PFDs based on expected structures and fit the Ansatze.

Comparison of $p\bar p \rightarrow jjj$ (in full color) to $pp \rightarrow Wjj$ (at leading color):
Kinematics # Poles ($W$) LCD Ansatz Partial-Fraction Ansatz Rational Functions
5-point massless 35 ~200k ~4k $\sim$200 KB
5-point 1-mass >200 >5M $\sim$40k $\sim$25 MB
$\displaystyle \kern-10mm \{W_j\} = \bigcup_{\sigma \; \in \; \text{Aut}(R_6)} \sigma \circ \big\{ \langle 12 \rangle, \langle 1|2+3|1], \langle 1|2+3|4], s_{123}, \Delta_{12|34|56}, ⟨3|2|5+6|4|3]-⟨2|1|5+6|4|2] \big\} $
Complexity of 2-loop 5-point 1-mass Amplitudes
$\circ$ The Ansatz size grows quickly with
multiplicity (m) and mass dimension (d):

$\displaystyle \small \left(\mkern -9mu \begin{pmatrix}\, m(m-3)/2 \, \\ \, d/2 \, \end{pmatrix} \mkern -9mu \right)$

is a lower bound. GDL, Maître ('20)
$\circ\,$ Compact residues for the new 2-loop (spurious?) pole, $⟨k|j|p\mkern-7.5mu/_V|l|k]-⟨j|i|p\mkern-7.5mu/_V|l|j]$, e.g.: $$r^{(5 \text{ of } 54)}_{\bar{u}^+g^+g^+d^-(V\rightarrow \ell^+ \ell^-)} = \frac{[12][23]⟨24⟩⟨46⟩^2⟨1|2+3|4]⟨2|1+3|4]}{⟨12⟩⟨23⟩⟨56⟩(⟨3|2|5+6|4|3]-⟨2|1|5+6|4|2])^2}$$
$\circ\,$ The three mass Grams, $\Delta_{12|34|p_V}, \Delta_{14|23|p_V}$, behave analogously to one-loop amplitudes, e.g.:
$$ r^{(73 \text{ of } 120)}_{\bar{u}^+g^-g^+d^-(V\rightarrow \ell^+ \ell^-)} = \frac{105}{128}\frac{⟨2|1+4|3]⟨4|2+3|1]⟨6|1+4|5]s_{14}s_{23}s_{56}{\color{green}(s_{124}-s_{134})}(s_{123}-s_{234})(s_{25}+s_{26}+s_{35}+s_{36})}{{\color{orange}⟨3|1+4|2]}{\color{red}Δ_{23|14|56}^4}} + \\ \Bigg[-6\frac{[12]^2⟨13⟩[25]⟨34⟩⟨36⟩⟨56⟩[56]{\color{green}(s_{124}-s_{134})}}{{\color{orange}⟨3|1+4|2]^5}}\Bigg] + \Bigg[ \; \Bigg]_{1234\rightarrow \overline{4321}}+ \mathcal{O}\left(\frac{1}{⟨3|1+4|2]^{4}Δ_{23|14|56}^{3}}\right)$$
Thank you
for your attention!

These slides are powered by:
markdown, html, revealjs, hugo, mathjax, github

Backup Slides

Constraints from Poles
Bootstrapping trees (?)

$\circ$ The degree of divergence / vanishing on various surfaces imposes strong constraints, e.g.
$ A^{\text{tree}}_{q^+g^+g^+\bar q^-g^-g^-} = \frac{\mathcal{N(\text{m.d.} = 6\,,\; \text{p.w.} = [-1, 0, 0, 1, 0, 0])}}{\langle 12\rangle\langle 23\rangle\langle 34\rangle [45][56][61]s_{345}}$
$\circ$ Pretend this is un unknown integral coefficient, $\mathcal{N}$ has 143 free parameters.
$\circ$ List the various prime ideal, such as




$ \big\langle \langle 12\rangle, \langle 23\rangle, \langle 13\rangle \big\rangle, \; \big\langle |1\rangle \big\rangle, \; \big\langle \langle 12\rangle, |1+2|3]\big\rangle, \dots$
$\phantom{\circ}$ and impose that $\mathcal{N}$ vanishes to the correct order. We determine it up to an overall constant.
GDL, Page ('22)
$\circ$ Likewise, the ansatz for $A^{\text{tree}}_{g^+g^+g^+ g^-g^-g^-}$ shrinks $1326 \rightarrow 1$, etc..




Effectively, we can compute trees, just from their poles orders.
Note: compared to BCFW there is no information about residues.

Partial Fraction Decompositions

$\circ$ For true integral coefficients, we can't rely on the Ansatz to shrinks to an overall constant.
$\circ$ Partial fraction decompositions (PFDs) are a popular method to tame algebraic complexity.
$\circ$ In my opinion, a PFD algorithm needs



$1.$ to say if two poles $W_a$ and $W_b$ are separable into different fractions;
$2.$ ideally, to answer $(1.)$ without having access to an analytic expression.
$\circ$ Hilbert's nullstellensatz: if $\mathcal{N}$ vanishes on all branches of $\langle W_a, W_b \rangle$, then the PFD is possible$\kern-3mm\phantom{x}^\dagger$.
$\circ$ Generalizing to powers $>\kern-1mm 1$ can be done via symbolic powers and the Zariski-Nagata Theorem.
GDL, Page ('22)
$\circ$ Similarly, generalizing to non-radical ideals requires ring extensions.
Campbell, GDL, Ellis ('22)
Issue: evaluations on singular surfaces are expensive, but are not always needed!
Opportunity: we get more than partial fraction decompositions.







$\kern-4mm\phantom{x}^\dagger$ $\langle W_a, W_b\rangle$ needs to be radical.

Beyond Partial Fractions

$\circ$ $\color{red}\text{Case 0}$: the ideal does $\color{green}\text{not involve denominator factors}$.
E.g. a 6-point function $c_i$ has a pole at $⟨1|2+3|4]$ but not at $⟨4|2+3|1]$,
yet it is regular on the irreducible surface $V(\big\langle ⟨1|2+3|4], ⟨4|2+3|1] \big\rangle)$. Then


$\displaystyle c_i \sim \frac{⟨4|2+3|1]}{⟨1|2+3|4]} + \mathcal{O}(⟨1|2+3|4]^0) \; \text{ instead of } \; c_i \sim \frac{1}{⟨1|2+3|4]} + \mathcal{O}(⟨1|2+3|4]^0)$
$\circ$ $\color{red}\text{Case 1}$: the $\color{green}\text{degree of vanishing is non-uniform}$ across branches, for example:

$\displaystyle \frac{s_{14}-s_{23}}{⟨1|3+4|2]⟨3|1+2|4]}$
has a double pole on the first branch, and a simple pole on the second branch of

$\big\langle⟨1|3+4|2], ⟨3|1+2|4]\big\rangle_{R_6} = \big\langle ⟨13⟩, [24] \big\rangle_{R_6} \cap \big\langle ⟨1|3+4|2], ⟨3|1+2|4], (s_{14}-s_{23})\big\rangle_{R_6}$
$\circ$ $\color{red}\text{Case 2}$: ideal is $\color{green}\text{non-radical}$ (example on last slide)


$\displaystyle \small \kern0mm \sqrt{\big\langle {\color{black}⟨3|1+4|2]}, {\color{black}Δ_{23|14|56}} \big\rangle_{R_6}} = \big\langle {\color{black}⟨3|1+4|2]}, {\color{black}s_{124}-s_{134}} \big\rangle_{R_6} $