Reconstruction of analytical amplitudes
across loops, legs and theories
arXiv:1904.04067 (JHEP) arXiv:1910.11355
Giuseppe De Laurentis
with Daniel Maître
IPPP Internal Seminar

Table of Contents
A. Reconstruction of analytical spinor-helicity amplitudes
1. Motivation 2. Singular limits 3. Partial fractions and ansatze
4. Rational coefficients in QCD
B. Tree amplitudes from the CHY formalism
1. Motivation 2. Scattering equations 3. CHY-Integrands 4. Amplitudes
A. Reconstruction of analytical
spinor-helicity amplitudes
A 1.1 Motivation
Cross sections at hadron colliders
$σ_{2 \rightarrow n - 2} = ∑_{a,b} ∫ dx_a dx_b f_{a/h_1}(x_a, μ_F) \, f_{b/h_2}(x_b, μ_F) \;\hat{σ}_{ab→n-2}(μ_F, μ_R)$
$d\hat{σ}_{n}=\frac{1}{2\hat{s}}dΠ_{n-2}\;(2π)^4δ^4\big(∑_{i=1}^n p_i\big)\;|\overline{\mathcal{A}(p_i,μ_F, μ_R)}|^2$
Better predictions require both more loops and higher multiplicity.
| |
|
||||
| 4 | 5 | 6 | 7 | ||
| loops | 0 | 2 | 3 | 4 | 5 |
| 1 | 4 | 5 | 6 | 7 | |
| 2 | 6 | 7 | 8 | 9 | |
Powers of coupling in pure gluon scattering.
Chromo-dynamics and kinematics
Color ordering at tree level and one loop [1, 2, …]:
$\mathcal{A}^{tree}_{n}({p_i, λ_i, a_i}) = \; g^{n-2} ∑_{σ\in S_n/Z_n} \text{Tr}(T^{a_σ(1)}\dots T^{a_σ(n)}) A^{tree}_n(σ(1^{λ_1}),\dots ,σ(n^{λ_n}))$
$\mathcal{A}^{1-loop}_{n}({p_i, λ_i, a_i}) = \; g^{n} ∑_{σ\in S_n/Z_n} N_{c} \text{Tr}(T^{a_σ(1)}\dots T^{a_σ(n)}) A_{n;1}(σ(1^{λ_1}),\dots ,σ(n^{λ_n}))$ $ + ∑_{c = 2}^{\lfloor n/2 \rfloor + 1}∑_{σ\in S_n/Z_{n;c}} \text{Tr}(T^{a_σ(1)}\dots T^{a_σ(c-1)})\text{Tr}(T^{a_σ( c)}\dots T^{a_σ(n)}) A_{n;c}(σ(1^{λ_1}),\dots ,σ(n^{λ_n}))$
Decomposition in terms of basis integrals [3, 4, 5, …]:
$$A^{1-loop}_{n;1} = \sum_i d_i I^i_{Box} + \sum_i c_i I^i_{Triangle} + \sum_i b_i I^i_{Bubble} + R$$
Intermediate and final expressions
Brute force calculations are a mess:

Results are often much easier [6, 7]:
$A^{tree}(1^{+}_{g}2^{+}_{g}3^{+}_{g}4^{-}_{g}5^{-}_{g}) = \frac{i\,⟨45⟩^{4}}{⟨12⟩⟨23⟩⟨34⟩⟨45⟩⟨51⟩}$
Numerical and Analytical: pros and cons
Numerical calculations efficiently bypass algebraic complexity, see:
But analytical results can still be useful, they can provide:
|
$\cdot$ faster computation $\cdot$ better numerical stability $\cdot$ easier to distribute than a program |
$\cdot$ possible to compile on a GPU $\cdot$ explicit analytical structure $…$ |
How can we access a (relatively) compact analytical final expression from numerical evaluations?
A 1.2 Spinor Helicity
Lowest-laying representations of the Lorentz group
(Recall: $\mathfrak{so}(1, 3)_\mathbb{C} \sim \mathfrak{su}(2) \times \mathfrak{su}(2)$)
| $\boldsymbol{(j_{-},j_{+})}$ | dim. | name | quantum field | kinematic variable |
|---|---|---|---|---|
| (0,0) | 1 | scalar | $h$ | m |
| (0,1⁄2) | 2 | right-handed Weyl spinor | $\chi_{R\,\alpha}$ | $\lambda_\alpha$ |
| (1⁄2,0) | 2 | left-handed Weyl spinor | $\chi_L^{\,\dot\alpha}$ | $\bar{\lambda}^{\dot\alpha}$ |
| (1⁄2,1⁄2) | 4 | rank-two spinor/four vector | $A^\mu/A^{\dot\alpha\alpha}$ | $P^\mu/P^{\dot\alpha\alpha}$ |
| (1⁄2,0)$\oplus$(0,1⁄2) | 4 | bispinor (Dirac spinor) | $\Psi$ | $u, v$ |
Spinors
Weyl spinors are sufficient for massless particles:
$\text{det}(P^{\dot\alpha\alpha})=m^2 \rightarrow 0 \quad \Longrightarrow \quad P^{\dot\alpha\alpha} = \bar\lambda^{\dot\alpha}\lambda^\alpha$.
In terms of 4-momentum components we have:
$$ \lambda_\alpha=\frac{1}{\sqrt{p^0+p^3}}\begin{pmatrix}p^0+p^3 \\ p^1+ip^2\end{pmatrix} \, , \;\;\; \lambda^\alpha=\epsilon^{\alpha\beta} \lambda_\beta =\frac{1}{\sqrt{p^0+p^3}}\begin{pmatrix}p^1+ip^2 \\ -p^0+p^3\end{pmatrix} $$
$\bar\lambda_{\dot\alpha}=\frac{1}{\sqrt{p^0+p^3}}\begin{pmatrix}p^0+p^3 \\ p^1-ip^2\end{pmatrix} \, , \;\;\; \bar\lambda^{\dot\alpha}=\epsilon^{\dot\alpha\dot\beta}\bar\lambda_{\dot\beta}=\frac{1}{\sqrt{p^0+p^3}}\begin{pmatrix}p^1-ip^2 \\ -p^0+p^3\end{pmatrix}$
$$ \bar\lambda_{\dot\alpha} = (\lambda_\alpha)^* \quad if \quad p^i \in \mathbb{R}; \quad \quad \bar\lambda_{\dot\alpha} \neq (\lambda_\alpha)^* \quad if \quad p^i \in \mathbb{C} $$
Spinor Helicity
$$ ⟨ij⟩ = λ_iλ_j = (λ_i)^α(λ_j)_α \quad \quad \quad [ij] = \barλ_i\barλ_j = (\barλ_i)_\dotα(\barλ_j)^\dotα $$
$$ s_{ij} = ⟨ij⟩[ji] $$
$$ ⟨i\;|\;(j+k)\;|\;l] = (λ_i)^α (\not P_j + \not P_k )_{α\dotα} \barλ_l^\dotα $$
$$ ⟨i\;|\;(j+k)\;|\;(l+m)\;|\;n⟩ = (λ_i)^α (\not P_j + \not P_k )_{α \dot α} (\bar{\not P_l} + \bar{\not P_m} )^{\dot α α} (λ_n)_α $$
$$ tr_5(ijkl) = tr(\gamma^5 \not P_i \not P_j \not P_k \not P_l) = [i\,|\,j\,|\,k\,|\,l\,|\,i⟩ - ⟨i\,|\,j\,|\,k\,|\,l\,|\,i] $$
Why use complex momenta?
We want to be able to distinguish between different poles.
For example, we want to tell apart:
$$ \frac{1}{⟨ij⟩} \quad and \quad \frac{1}{[ji]} $$
but with real momenta we would have:
$$ ⟨ij⟩ \sim [ji]^* \sim \sqrt{s_{ij}} $$
A 2.1 Singular limits
Singular limits $\Rightarrow$ poles of the amplitude
We need a set of Lorentz invariants:
$r_i \in \{ ⟨12⟩, ⟨13⟩, \dots, ⟨1|2+3|4], \dots, s_{123}, \dots \}$,
and let $\, \mathbb{f} \,$ be the function we want to reconstruct.
$r_i \rightarrow ε \ll 1, \quad r_{j \neq i} \sim \mathcal{O}(1), \quad \mathbb{f} \rightarrow ε^α \; \Rightarrow \; log(\mathbb{f}) \rightarrow α\cdot log(ε)$
Tree-level example
$\mathbb{f} = A^{tree}(1^{+}_{g}2^{+}_{g}3^{+}_{g}4^{-}_{g}5^{-}_{g}6^{-}_{g})$
| |
|
 |
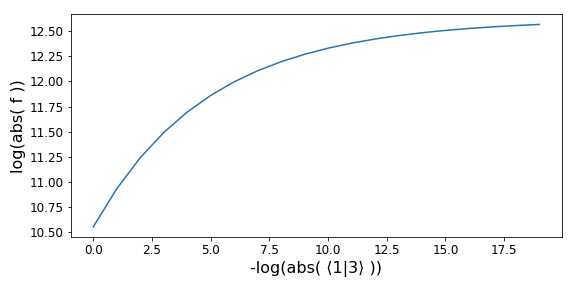 |
Note: the invariant on the x-axis gets smaller from left to right.
The least common denominator
Studying all the limits yields the least common denominator for $\mathbb{f}$:
$\mathbb{f} = \frac{\mathcal{N_{LCD}}}{\mathcal{D_{LCD}}} = \frac{\mathcal{N_{LCD}}}{⟨12⟩⟨16⟩[16]⟨23⟩⟨34⟩[34][45][56]s_{234}s_{345}}$.
The complexity of the numerator depends on two parameters:
- mass dimension; $\quad \quad \quad$ 2. little group scalings.
The ansatz has 1326 independent terms.
A 2.2 Doubly singular limits
Partial fractioning
Except for the easiest cases, we should really think about $\mathbb{f}$ as:
$\mathbb{f} = \sum_i \frac{\mathcal{N}_i}{\mathcal{D}_i} = \sum_i \frac{\mathcal{N}_i}{\mathcal{R}_i\mathcal{S}_i}$,
where $\mathcal{R}_i$ are products of subsets of $\mathcal{D_{LCD}}$ (i.e. real poles),
and $\mathcal{S}_i$ are products of factors not in $\mathcal{D_{LCD}}$ (i.e. spurious poles).
Doubly singular limits
The required information can be accessed from doubly singular limits.
We now want phase space points where two invariants vanish:
$r_i \rightarrow ε \ll 1, \quad r_j \rightarrow ε \ll 1, \quad \mathbb{f} \rightarrow ε^α \; \Rightarrow \; log(\mathbb{f}) \rightarrow α\cdot log(ε)$
In general we cannot guarantee uniqueness anymore,
even with complex momenta.
$\exists \;r_{k \neq i, j} \sim \epsilon$.
Information from doubly singular limits
| ⟨1|2⟩ | ⟨1|6⟩ | [1|6] | ⟨2|3⟩ | ⟨3|4⟩ | [3|4] | [4|5] | [5|6] | s_234 | s_345 | |
|---|---|---|---|---|---|---|---|---|---|---|
| ⟨1|2⟩ | 1 | 1, 30 | 1, 3 | 1, 31 | 1, 2 | 2, 12 | 2, 3 | 2, 10 | 1, 2 | 2, 10 |
| ⟨1|6⟩ | 1, 30 | 1 | 1, 2 | 1, 2 | 1, 10 | 2, 4 | 2, 12 | 1, 3 | 2, 10 | 2, 10 |
| |
||||||||||
| s_234 | 1, 2 | 2, 10 | 2, 10 | 2, 10 | 2, 10 | 2, 10 | 1, 2 | 2, 10 | 1 | 1, 2 |
| s_345 | 2, 10 | 2, 10 | 2, 10 | 1, 2 | 2, 10 | 2, 10 | 2, 10 | 1, 2 | 1, 2 | 1 |
The first number is the slope of the log-log plot in the limit,
the second number is the degeneracy of the phase space in the limit.
Let’s introduce the following notation, which we’ll need later: $\{a, b\}_\epsilon$.
It represents the set of all invariants that vanish when $a$ and $b$ vanish.
For example:
$\{⟨12⟩,\,⟨16⟩\}_\epsilon = \{ ⟨12⟩, ⟨16⟩, ⟨26⟩, s_{345}, ⟨2|1+6|5], \dots \text{25 more} \dots \}$
Which poles share the same denominator?
The following is single line of the table in the previous slide:
| ⟨1|2⟩ | ⟨1|6⟩ | [1|6] | ⟨2|3⟩ | ⟨3|4⟩ | [3|4] | [4|5] | [5|6] | s_234 | s_345 | |
|---|---|---|---|---|---|---|---|---|---|---|
| s_234 | 1 , 2 | 2 , 10 | 2 , 10 | 2 , 10 | 2 , 10 | 2 , 10 | 1 , 2 | 2 , 10 | 1 | 1 , 2 |
Diagramatic representation of relation between poles
A 3.1 Partial fraction decomposition
Partial fraction decomposition #1
| |
|
(Spoiler: $ \quad \small \mathcal{N_1} = 1i⟨4|2+3|1]^3, \quad \mathcal{N_2} = -1i⟨6|1+2|3]^3$)
Where does $⟨2|1+6|5]$ come from?
$\{⟨12⟩, [56]\}_{\epsilon} \, \cap \, \{⟨16⟩, s_{234}\}_{\epsilon} \, \cap \, \{⟨23⟩, [45]\}_{\epsilon} \, \cap \, \{[34], s_{234}\}_{\epsilon} \, \dots$
Partial fraction decomposition #2
| |
|
(Spoiler: $ \quad \small \mathcal{N_1} = 1i[23]^3⟨56⟩^3, \quad \mathcal{N_2} = -1i[12]^3⟨45⟩^3, \quad \mathcal{N_3} = 1is_{123}^3 $)
$⟨1|2+3|4] = \{⟨12⟩, [34]\}_{\epsilon} \, \cap \, \{⟨23⟩, s_{234}\}_{\epsilon} \, \cap \, \{⟨16⟩, [45]\}_{\epsilon} \, \cap \, \dots$ $⟨3|1+2|6] = \{⟨23⟩, [16]\}_{\epsilon} \, \cap \, \{⟨12⟩, s_{345}\}_{\epsilon} \, \cap \, \{⟨34⟩, [56]\}_{\epsilon} \, \cap \, \dots$
Both of these partial fractions correspond to some BCFW shift,
but we are not limited to these representations.
Partial fraction decomposition #3
| |
|
We now have no spurious poles, but $s_{234}$ and $s_{345}$ appear in the same denominator, although the doubly singular limit suggests they shouldn’t.
This means that in the limit of $\{s_{234}, s_{345}\} \rightarrow \epsilon$ the individual terms will behave like $\epsilon^{-2}$ but the sum as $\epsilon^{-1}$.
Different representations can be exploited to ensure numerical stability.
A 3.2 Fitting of ansatz
Spinor ansatz
Let’s consider the first representation:
$\mathbb{f}=$ $\frac{\mathcal{N_1}}{[16]⟨23⟩⟨34⟩[56]⟨2|1+6|5]s_{234}}+$ $\frac{\mathcal{N_2}}{⟨12⟩⟨16⟩[34][45]⟨2|1+6|5]s_{345}}$
$\mathcal{N_1}$ has mass dimension: 6, and phase weights: [-3, 0, 0, 3, 0, 0].
The ansatz has size 10:
$[⟨24⟩⟨24⟩⟨24⟩[12][12][12],$ $⟨24⟩⟨24⟩⟨34⟩[12][12][13],$ $⟨24⟩⟨24⟩⟨45⟩[12][12][15],$ $⟨24⟩⟨34⟩⟨34⟩[12][13][13],$ $⟨24⟩⟨34⟩⟨45⟩[12][13][15],$ $⟨24⟩⟨45⟩⟨45⟩[12][15][15],$ $⟨34⟩⟨34⟩⟨34⟩[13][13][13],$ $⟨34⟩⟨34⟩⟨45⟩[13][13][15],$ $⟨34⟩⟨45⟩⟨45⟩[13][15][15],$ $⟨45⟩⟨45⟩⟨45⟩[15][15][15]]$,
much smaller than the one for $\mathcal{N_{LCD}}$
which had more than 1000 terms!
Gaussian elimination
$\mathbb{f}=$ $\frac{\mathcal{N_1}}{[16]⟨23⟩⟨34⟩[56]⟨2|1+6|5]s_{234}}+$ $\frac{\mathcal{N_2}}{⟨12⟩⟨16⟩[34][45]⟨2|1+6|5]s_{345}}$
Isolate the first term by generating phase space points
in the limit of, say, $s_{234} \rightarrow \epsilon$.
Then we can reconstruct the numerical coefficient of the ansatz entries by Gaussian elimination.
$$ M_{ij}c_j = \mathbb{f}(P_i) \quad \text{i.e.} \quad \begin{pmatrix} \leftarrow ansatz(P_1) \rightarrow \\ \leftarrow ansatz(P_2) \rightarrow \\ \dots \end{pmatrix} \cdot \begin{pmatrix} c_1 \\ c_2 \\ \dots \end{pmatrix} = \begin{pmatrix} \mathbb{f}(P_1) \\ \mathbb{f}(P_2) \\ \dots \end{pmatrix} $$
We get:
$⟨24⟩⟨24⟩⟨24⟩[12][12][12]: 1i$, $⟨24⟩⟨24⟩⟨34⟩[12][12][13]: 3i$,
$⟨24⟩⟨34⟩⟨34⟩[12][13][13]: 3i$, $⟨34⟩⟨34⟩⟨34⟩[13][13][13]: 1i$
How big is the ansatz?
Easiest to count at constant null phase weights;
the size of the ansatz is a function of:
1. its mass dimension ($d$) $\quad\quad$ 2. multiplicity of phase space ($m$).
If we allow only for a polynomial in the numerator, then:
$|s_{ij}| = \frac{m(m-3)}{2}$ $\quad\quad$ $|tr_5| = {m-1 \choose 4}$
$\left(\mkern -9mu \begin{pmatrix}\, |s_{ij}| \, \\ \, d/2 \, \end{pmatrix} \mkern -9mu \right) \leq$ ansatz size $\leq \left(\mkern -9mu \begin{pmatrix} \, |s_{ij}| \, \\ \, d/2 \, \end{pmatrix} \mkern -9mu \right) + |tr_5| \left(\mkern -9mu \begin{pmatrix} \, |s_{ij}| \, \\ \, (d-4)/2 \, \end{pmatrix} \mkern -9mu \right)$
The upper bound is saturated for $(\forall m \wedge d \leq 4)$ and for $(\forall d \wedge m \leq 5)$.
Otherwise it is an overcounting due to Schouten identity for 4-momenta:
$tr_5(2345)1_\mu - tr_5(1345)2_\mu + tr_5(1245)3_\mu - tr_5(1235)4_\mu + tr_5(1234)5_\mu = 0$
A 4.1 Rational coefficients in QCD
Six-gluon one-loop rational coefficients
As an application we obtained analytical expressions for all parts of the six-gluon amplitude with a gluon in the loop.
All independent coefficients are available as anchillary files at: arXiv:1904.04067.
Our expressions are manifestly rational and gauge invariant.
For a summary of the litterature see Ref.15.
Three mass triangle
$\mathcal{D_{LCD}} = ⟨12⟩[12]⟨34⟩[34]⟨56⟩[56]⟨1|3+4|2]^4⟨3|1+2|4]^4⟨5|1+2|6]^4Δ_{135}^3$
An expression was previously obtained in [16].
We obtain an explicitly rational expression, like for $\mathcal{N}=1$ SUSY in [17].
Pole structure
| |
$123456$ $\overline{216543}$ $345612$ $\overline{432165}$ $561234$ $\overline{654321}$ |
| ⟨12⟩ | [12] | ⟨34⟩ | [34] | ⟨56⟩ | [56] | ⟨1|3+4|2] | ⟨3|1+2|4] | ⟨5|1+2|6] | Δ_135 | |
|---|---|---|---|---|---|---|---|---|---|---|
| ⟨1|2⟩ | 1 | 1, 2 | 1, 2 | 2, 12 | 1, 2 | 2, 12 | 4, 4 | 5, 6 | 2, 10 | 2, 4 |
| |
||||||||||
| ⟨3|1+2|4] | 5, 6 | 2, 10 | 4, 4 | 4, 4 | 2, 10 | 5, 6 | 4, 2 | 4 | 4, 2 | 3.5, 4 |
| |
||||||||||
Do we need square roots of momentum invariants?
All branch cuts should have been taken care of by unitarity cuts.
We should be able to explain this without using square roots.
The culprit is $\Delta$, which first appears in the
three mass triangle momentum parametrisation:
$\Delta_{135} = (K_1 \cdot K_2)^2 - K_1^2 K_2^2$
Solution:
In some limits $\Delta$ behaves like the square of some quantity
$(\Omega_{351})^2 \equiv (2s_{12}s_{56}-(s_{12}+s_{56}-s_{45})s_{123})^2 = 4s_{123}^2\Delta_{135}-4s_{12}s_{56}\langle 4|1+2|3]\langle 3|1+2|4]$
$(\Pi_{351})^2 \equiv (s_{123}-s_{124})^2 = 4\Delta_{135}-4\langle 4|1+2|3]\langle 3|1+2|4]$
The three-mass triangle rational coefficient
$$
\begin{gathered}
\scriptscriptstyle \frac{-1/2i⟨23⟩^3[45]^3s_{123}^2Ω_{351}}{⟨12⟩[56]⟨1|2+3|4]⟨3|1+2|4]^4⟨3|1+2|6]}+\\
\scriptscriptstyle \frac{1/4i[12]⟨23⟩^3[45]^3⟨56⟩⟨4|1+2|3]s_{123}Π_{351}}{⟨1|2+3|4]⟨3|1+2|4]^3⟨3|1+2|6]Δ_{135}}+\\
\scriptscriptstyle \frac{2i⟨23⟩^2[45]^2⟨2|1+3|5]s_{123}Ω_{351}}{⟨12⟩[56]⟨1|2+3|4]⟨3|1+2|4]^3⟨3|1+2|6]}+\\
\scriptscriptstyle \frac{⟨2|3+4|1]⟨6|1+2|5]Ω_{351}(1i⟨12⟩[12]⟨13⟩[13]\,…⟪4\,\text{terms}⟫…\, -1i⟨23⟩[23]⟨35⟩[35])}{⟨1|3+4|2]⟨3|1+2|4]^2⟨5|1+2|6]Δ_{135}}+\\
\scriptscriptstyle \frac{4i⟨12⟩^3[12]^2[13][15]⟨36⟩\,…⟪65\,\text{terms}⟫…\, -4i[12]⟨23⟩^2[23]⟨26⟩[35]⟨36⟩[36]}{⟨1|3+4|2]⟨3|1+2|4]^2⟨5|1+2|6]}+\\
\scriptscriptstyle \frac{[12]⟨23⟩^3[45]^3⟨56⟩⟨4|1+2|3]^2Π_{351}(1/8is_{123}+1/16is_{124})}{⟨1|2+3|4]⟨3|1+2|4]^2⟨3|1+2|6]Δ_{135}^2}+\\
\scriptscriptstyle \frac{-3i⟨23⟩[45]⟨2|1+3|5]^2Ω_{351}}{⟨12⟩[56]⟨1|2+3|4]⟨3|1+2|4]^2⟨3|1+2|6]}+\\
\scriptscriptstyle \frac{⟨23⟩[45](-4i⟨12⟩^2[12]^2[15]⟨26⟩\,…⟪31\,\text{terms}⟫…\, +4i[12]⟨26⟩^2⟨56⟩[56]^2)}{⟨1|2+3|4]⟨3|1+2|4]^2⟨3|1+2|6]}+\\
\scriptscriptstyle \frac{5/32i⟨12⟩[12]⟨34⟩[34]⟨56⟩[56]⟨2|3+4|1]⟨4|1+2|3]⟨6|1+2|5]Π_{351}}{⟨1|3+4|2]⟨3|1+2|4]⟨5|1+2|6]Δ_{135}^2}+\\
\scriptscriptstyle \frac{⟨2|3+4|1]⟨4|1+2|3]⟨6|1+2|5]⟨1|3+4|1]⟨56⟩[56](-1/4i⟨12⟩[12]⟨23⟩[23]\,…⟪17\,\text{terms}⟫…\, +1/4i⟨24⟩[24]⟨34⟩[34])}{⟨1|3+4|2]⟨3|1+2|4]⟨5|1+2|6]Δ_{135}^2}+\\
\dots\\
\scriptscriptstyle (123456\; \rightarrow \; 345612)+\\
\scriptscriptstyle (123456\; \rightarrow \; 561234)+\\
\dots
\end{gathered}
$$
A six-gluon one-loop rational part
$R^{1-loop}_6(1^{+}_{g}2^{-}_{g}3^{+}_{g}4^{-}_{g}5^{+}_{g}6^{-}_{g})$
$\mathcal{D_{LCD}} =$ $⟨12⟩[12]⟨13⟩^2⟨15⟩^2⟨16⟩[16]⟨23⟩[23][24]^2[26]^2⟨34⟩[34]⟨35⟩^2⟨45⟩[45][46]^2⟨56⟩[56]$ $⟨1|2+3|1]^2⟨1|5+6|1]^2⟨1|3+4|2]^2⟨1|2+3|6]^2⟨2|1+6|2]^2⟨2|3+4|2]^2$ $⟨3|1+6|2]^2⟨3|1+2|3]^2⟨3|4+5|3]^2⟨3|1+2|4]^2⟨4|2+3|4]^2⟨4|5+6|4]^2$ $⟨5|1+6|4]^2⟨5|1+6|5]^2⟨5|3+4|5]^2⟨5|1+2|6]^2⟨6|1+2|6]^2⟨6|4+5|6]^2$ $s_{123}s_{234}s_{345}Δ_{135}^2Δ_{624}^2$
The mass dimension is now 116,
which would imply an ansatz with size roughly $10^{10}$.
An analytical expression for this component was previously obtained in [18] from Feynman diagrams.
The pole structure
is a bit of a mess:
The rational part
$$
\begin{gathered}
\scriptscriptstyle\frac{2/3i⟨12⟩^3[15]^3[23]s_{123}}{[45]⟨1|2+3|1]^2⟨1|2+3|4]⟨1|2+3|6]⟨3|1+2|6]}+\\
\scriptscriptstyle\frac{-2/3i⟨12⟩^3[15]^3[23]⟨3|1+2|5]}{⟨13⟩[45][56]⟨1|2+3|1]^2⟨1|2+3|4]⟨3|1+2|6]}+\\
\scriptscriptstyle\frac{1i⟨12⟩^3[15]^2⟨23⟩[23]^2[56]}{[45]⟨1|2+3|1]⟨1|2+3|4]⟨1|2+3|6]^2⟨3|1+2|6]}+\\
\scriptscriptstyle\frac{⟨12⟩^2[15]^2[23](-1i⟨12⟩[15]+2i⟨23⟩[35])}{[45]⟨1|2+3|1]⟨1|2+3|4]⟨1|2+3|6]⟨3|1+2|6]}+\\
\scriptscriptstyle\frac{1i⟨12⟩^3[15]^2[25]⟨3|1+2|5]}{⟨13⟩^2[45][56]⟨1|2+3|1]⟨1|2+3|4]⟨3|1+2|6]}+\\
\scriptscriptstyle\frac{2i⟨12⟩^2[15]^2[35]⟨3|1+2|5]}{⟨13⟩[45][56]⟨1|2+3|1]⟨1|2+3|4]⟨3|1+2|6]}+\\
\scriptscriptstyle\frac{-1i⟨12⟩^2[15]⟨23⟩[25]^2⟨2|1+3|5]}{⟨13⟩^2[45][56]⟨1|2+3|4]⟨3|1+2|6]s_{123}}+\\
\scriptscriptstyle\frac{-1i⟨12⟩^2[15]^2[25]⟨2|1+3|5]}{⟨13⟩[45][56]⟨1|2+3|4]⟨3|1+2|6]s_{123}}+\\
\scriptscriptstyle\frac{⟨24⟩^2⟨26⟩^2(-1/6i⟨13⟩^2[13]⟨46⟩\,…⟪2\,\text{terms}⟫…\, +1/3i[12]⟨14⟩⟨16⟩⟨23⟩)}{⟨12⟩⟨16⟩⟨23⟩⟨34⟩⟨45⟩⟨56⟩⟨1|2+3|4]⟨3|1+2|6]}+\\
\scriptscriptstyle(123456\; \rightarrow \; \overline{234561})+
\scriptscriptstyle(123456\; \rightarrow \; 345612)+
\scriptscriptstyle(123456\; \rightarrow \; \overline{456123})+
\scriptscriptstyle(123456\; \rightarrow \; 561234)+
\scriptscriptstyle(123456\; \rightarrow \; \overline{612345})+\\
\scriptscriptstyle(123456\; \rightarrow \; \overline{654321})+
\scriptscriptstyle(123456\; \rightarrow \; 543216)+
\scriptscriptstyle(123456\; \rightarrow \; \overline{432165})+
\scriptscriptstyle(123456\; \rightarrow \; 321654)+
\scriptscriptstyle(123456\; \rightarrow \; \overline{216543})+
\scriptscriptstyle(123456\; \rightarrow \; 165432)+\\
\dots
\end{gathered}
$$
Five-partons two-loop remainders (preliminary results)
The same strategy can be applied to other rational coefficients,
e.g. two-loop finite remainders given in [19].
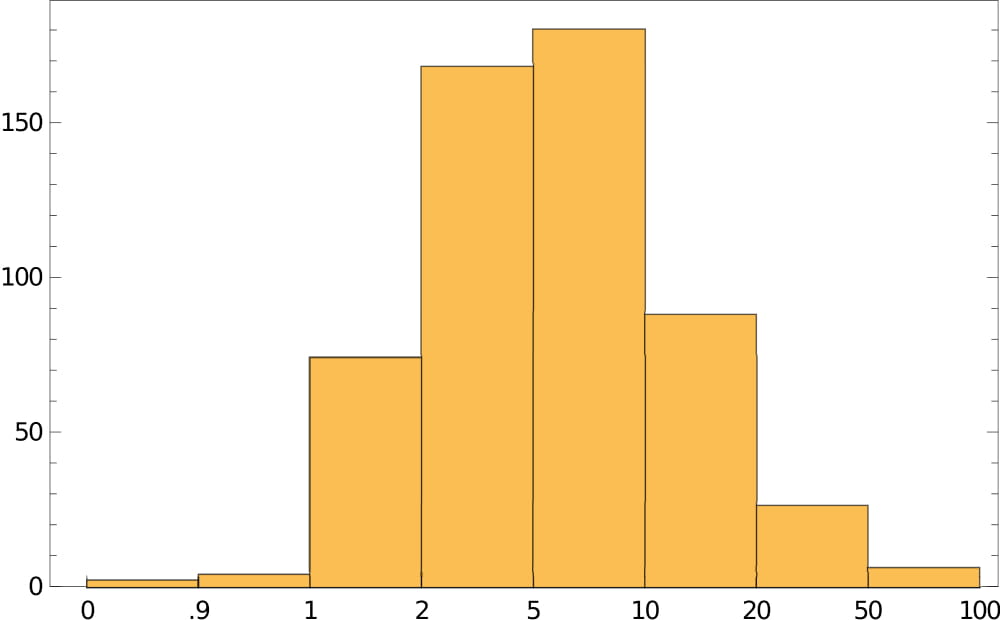
Showing ratio of leaf counts for Mandelstam and spinor-helicity expressions (x-axis) vs. frequency (y-axis). The complexity is significantly reduced.
Example: uubggg pmpmp Nf1 #3

and
$ -\frac{[32]^3 [41]^3}{2 [31]^3 [42]^3} $
are equivalent.
B. Tree amplitudes from the
CHY Formalism
B 1.1 Motivation
Hidden relations …
Relations between amplitudes in different theories are often hidden in a standard Lagrangian quantum field theory formulation.
$\mathcal{L_{Einstein Gravity}} = R\sqrt{-g} \quad \quad \mathcal{L_{Yang Mills}} = -\frac{1}{4}F^{a\mu\nu}F^{a}_{\mu\nu}$
$\mathcal{L_{Biadjoint Scalar}} = 2∂^µΦ^{aa′}∂_µΦ^{aa′}+\frac{y}{3}f^{abc}\tilde f^{a′b′c′}Φ^{aa′}Φ^{bb′}Φ^{cc′}$
E.g. the above are related by the KLT relations [20],
more generally known as double copy relations.
.. are made explicit
By comparison in the CHY formalism [21, 22, 23] these relations are made explicit in the structure of the CHY-Integrands:
$I_{CHY, Einstein Gravity} = PF’(\Psi) \; PF’(\tilde\Psi)$
$I_{CHY, Yang Mills} = C_n \; PF’(\Psi) \quad \quad I_{CHY, Biadjoint Scalar} = C_n \; C_n$
Loosely speaking we have [24]:
$A = \int I_{CHY} \quad$ and $\quad A_{EG} = A_{YM} \tilde A_{YM} / A_{BS}$
Independent formulation
$\circ$ it does not rely on the Lagrangian or Feynman diagrams;
$\circ$ it is more efficient than a brute-force computation;
$\circ$ it is less efficient than recursion relations;
$\circ$ but the latter in some cases are not available.
B 1.2 General Introduction
Scattering equations and Riemann sphere
The backbone of the CHY formalism are the scattering equations:
$f_a (z, k) \equiv \sum\limits_{b \in A \backslash \{a\}} \frac{k_a \cdot k_b}{z_a - z_b} = 0, \qquad \forall a \in A = \{1, \dots, n\}$
The $k$’s are the momenta, and the $z$’s live on the Riemann sphere.
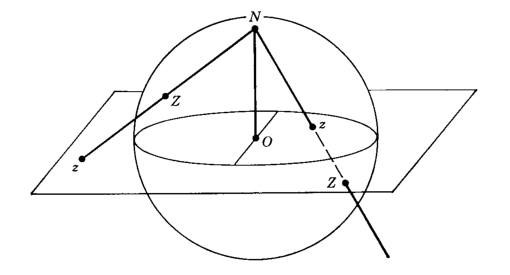
Möbius invariance or redundancy
The scattering equations $f_a$ are invariant under Möbius transformations:
$z \rightarrow \zeta = \frac{\alpha z + \beta}{\gamma z + \delta}$.
A Möbius transformation is obtained by performing the following operations on the Riemann sphere:
| 1) Translation $z \rightarrow \zeta = z + A$ | 2) Inversion $z \rightarrow \zeta = 1/z$ |
| 3) Rescaling $z \rightarrow \zeta = Bz$ | 4) Translation $z \rightarrow \zeta = z + C$ |
In general this allows us to fix three of the $z$’s:
$z_1 = \infty, \quad z_2 = 1, \quad z_n = 0 \;$
Amplitudes from integrals
The scattering amplitudes $\textit{A}_n$ are given by:
$\textit{A}_n \, = \, i \int \frac{d^nz}{d\omega} \;\; I_{\scriptscriptstyle CHY}(z; k; \epsilon) \prod’_{a \in A} \delta(f_a(z, k))$
$\; = \, i \oint_\textit{O} \frac{d^nz}{d\omega} \;\; I_{\scriptscriptstyle CHY}(z; k; \epsilon) \prod’_{a \in A}\frac{1}{f_a(z,k)}$
With the following definitions:
$d\omega = \frac{dz_rdz_sdz_t}{(z_r-z_s)(z_s-z_t)(z_t-z_s)}$
$\prod’_{a \in A} = (z_i-z_j)(z_j-z_k)(z_k-z_i)\prod_{a \in A \backslash \{i,j,k\}}$
which make $\textit{A}_n$ independent of the choice of $\{i, j, k\}$ and $\{r, s, t\}$.
Amplitudes from sums
In practice we want an algebraic equation of the amplitudes.
Change variables $z_a \rightarrow f_a$, $\,$ pick up a Jacobian:
$$ϕ_{ab}\, = \frac{∂ f_a}{∂ z_b}=
\begin{cases}
\frac{2 k_a \cdot k_b}{(z_a - z_b)^2} & a \neq b \; ,\\
- \sum\limits_{j \in A \backslash {a}} \frac{2 k_a \cdot k_j}{(z_a - z_j)^2} & a = b \; .
\end{cases}$$
Integrate over the delta functions, set $\{z_1, z_2, z_3\} = \{\infty, 1, 0\}$ get:
$\textit{A}_n \, = \, z_1^4 \cdot i \sum_{j = 1}^{(n-3)!} \frac{I_{\scriptscriptstyle CHY}(z^{(j)}(k); k; ϵ)}{\det(ϕ_{rst}^{ijk})(z^{(j)}(k); k)}$
B 2. The scattering equations
The original scattering equations
This part of the computation depends only on the scattering multiplicity!
No information about the thoery is required.
Solving the scattering equations (SE) is not trivial.
$f_a (z, k) \equiv \sum\limits_{b \in A \backslash \{a\}} \frac{k_a \cdot k_b}{z_a - z_b} = 0, \qquad \forall a \in A = \{1, \dots, n\}$
If we simply take the common denominator we obtain a polynomial of much higher degree than necessary.
The polynomial scattering equations
Instead we are going to consider the polynomial SE $h_{m}$ from [25]
$h_{m} = \sum_{S \subset A’,\, |S| = m} k^2_{S_1}z_S=0 \, , \quad \text{with} \quad 1 \leq m \leq n - 3 \, ,$
$A’ = A \backslash \{1,n\} \, , \quad S_1 = S \cup {1}$
$k_S = \sum_{b \in S} k_b \quad \text{and} \quad z_S = \prod_{b \in S} z_b$
For example, for $n = 5$:
$h_1 = z_2 k_{\{1,2\}}^2+z_3 k_{\{1,3\}}^2+z_4 k_{\{1,4\}}^2$
$h_2 = z_2 z_3 k_{\{1,2,3\}}^2+z_2 z_4 k_{\{1,2,4\}}^2+z_3 z_4 k_{\{1,3,4\}}^2$
Elimination theory
Needed for solving systems of polynomial equations.
Just like Gaussian elimination is used for the linear case.
We can rewrite the two polynomial SE for $n = 5$ as:
$$
\left(
\begin{array}{cc}
H & H^{z_2} \\
\end{array}
\right)|_{z_2=0} \cdot
\left(
\begin{array}{c}
1\\
{z_2}\\
\end{array}
\right)=
\left(
\begin{array}{cc}
z_3 s_{13}+ z_4 s_{14} & s_{12} \\
z_3 z_4 s_{134} & z_3 s_{123} + z_4 s_{124} \\
\end{array}
\right) \cdot
\left(
\begin{array}{c}
1\\
{z_2}\\
\end{array}
\right)=0$$
Using the following simplified notation:
$$
H = \left(
\begin{array}{c}
h_1 \\
h_2 \\
\end{array}
\right) \; , \quad
H^{\sigma _2} = \partial_{z_2}
\left(
\begin{array}{c}
h_1 \\
h_2 \\
\end{array}
\right) \; , \quad
k_{\{i,j,\dots\}}^2 = s_{ij\dots}
$$
Five-point solutions
Now taking the determinant of the matrix form of the SE we get:
$$
\det \left(
\begin{array}{cc}
H & H^{z_2} \\
\end{array}
\right)|_{z_2=0} = 0
$$
$$ z_3^2 s_{13} s_{123} + z_4 z_3 ( s_{14} s_{123} + s_{13} s_{124} - s_{12} s_{134} ) + z_4^2 s_{14} s_{124} = 0 \; , $$
This is the required quadratic in $ z_4 / z_3 $ .
By reintroducing $z_2$ and setting it to 1 we can then solve for $z_4$ and $z_3$:
$$ z_3 = \frac{-s_{12} s_{134} + s_{123} s_{14} - s_{124} s_{13} \pm \sqrt{s_{12}^2 s_{134}^2 - 2 s_{12} s_{123} s_{134} s_{14} - 2 s_{12} s_{124} s_{13} s_{134} + s_{123}^2 s_{14}^2 - 2 s_{123} s_{124} s_{13} s_{14} + s_{124}^2 s_{13}^2}}{2 s_{13} s_{134}} $$ $$ z_4 = \frac{-s_{12} s_{134} - s_{123} s_{14} + s_{124} s_{13} \mp \sqrt{s_{12}^2 s_{134}^2 - 2 s_{12} s_{123} s_{134} s_{14} - 2 s_{12} s_{124} s_{13} s_{134} + s_{123}^2 s_{14}^2 - 2 s_{123} s_{124} s_{13} s_{14} + s_{124}^2 s_{13}^2}}{2 s_{14} s_{134}} $$
What happens at six point?
Now we have three polynomial scattering equations:
$$
\mkern-30mu H = \left(
\begin{array}{c}
h_1 \\
h_2 \\
h_3 \\
\end{array}
\right) =
\left[\begin{matrix}s_{12} z_{2} + s_{13} z_{3} + s_{14} z_{4} + s_{15} z_{5} \\ s_{123} z_{2} z_{3} + s_{124} z_{2} z_{4} + s_{125} z_{2} z_{5} + s_{134} z_{3} z_{4} + s_{135} z_{3} z_{5} + s_{145} z_{4} z_{5} \\ s_{1234} z_{2} z_{3} z_{4} + s_{1235} z_{2} z_{3} z_{5} + s_{1245} z_{2} z_{4} z_{5} + s_{1345} z_{3} z_{4} z_{5}\end{matrix}\right]
$$
We want to eliminate 4 variables: $$ \{1, z_2\} \otimes \{1, z_3\} = \{1, z_2, z_3, z_2 z_3\} $$
But we only have 3 equations:
$$ \{h_1, h_2, h_3\} $$
Completing the system of equations
The solution is to introduce new variables and new equations:
$$ \{1, z_3\} \otimes \{1, z_2, z_3, z_2 z_3\} = \{1, z_2, z_3, z_2 z_3, z_3^2, z_2 z_3^2\} $$
$$ \{1, z_3\} \otimes \{h_1, h_2, h_3\} = \{h_1, h_2, h_3, z_3 h_1, z_3 h_2, z_3 h_3\} $$
Now we have the same number of equations and variables, write:
$$
\left(
\begin{array}{cc}
H & H^{z_2} & H^{z_3} & H^{z_2z_3} & 0 & 0 \\
0 & 0 & H & H^{z_2} & H^{z_3} & H^{z_2z_3} \\
\end{array}
\right)\Big|_{z_2=0, z_3=0} \cdot
\left(\begin{array}{c}
1\\
{z_2}\\
{z_3}\\
{z_2 z_3}\\
{z_3^2}\\
{z_2 z_3^2}\\
\end{array}
\right) = 0
$$
$$
$$
$$
\left(\begin{matrix}s_{14} z_{4} + s_{15} z_{5} & s_{12} & s_{13} & 0 & 0 & 0\\
s_{145} z_{4} z_{5} & s_{124} z_{4} + s_{125} z_{5} & s_{134} z_{4} + s_{135} z_{5} & s_{123} & 0 & 0\\
0 & s_{1245} z_{4} z_{5} & s_{1345} z_{4} z_{5} & s_{1234} z_{4} + s_{1235} z_{5} & 0 & 0\\
0 & 0 & s_{14} z_{4} + s_{15} z_{5} & s_{12} & s_{13} & 0\\
0 & 0 & s_{145} z_{4} z_{5} & s_{124} z_{4} + s_{125} z_{5} & s_{134} z_{4} + s_{135} z_{5} & s_{123}\\
0 & 0 & 0 & s_{1245} z_{4} z_{5} & s_{1345} z_{4} z_{5} & s_{1234} z_{4} + s_{1235} z_{5}\end{matrix}\right) \cdot
\left(\begin{array}{c}
1\\
{z_2}\\
{z_3}\\
{z_2 z_3}\\
{z_3^2}\\
{z_2 z_3^2}\\
\end{array}
\right) = 0
$$
Problem: the determinant is sextic

Abel–Ruffini theorem: no algebraic solution for order higher than 4.
In general: $\;$ order det $\;\sim\;$ # of SE solutions $\;\sim\;$ $(n-3)!$
Solution: use a numerical root-finding algorithm
Two open source packages: seampy, lips
>>> hms(6)
⎡ s₁₂⋅z₂ + s₁₃⋅z₃ + s₁₄⋅z₄ + s₁₅⋅z₅ ⎤
⎢s₁₂₃⋅z₂⋅z₃ + s₁₂₄⋅z₂⋅z₄ + s₁₂₅⋅z₂⋅z₅ + s₁₃₄⋅z₃⋅z₄ + s₁₃₅⋅z₃⋅z₅ + s₁₄₅⋅z₄⋅z₅⎥
⎣ s₁₂₃₄⋅z₂⋅z₃⋅z₄ + s₁₂₃₅⋅z₂⋅z₃⋅z₅ + s₁₂₄₅⋅z₂⋅z₄⋅z₅ + s₁₃₄₅⋅z₃⋅z₄⋅z₅ ⎦>>> oParticles = Particles(6)
>>> num_ss = {str(s): oParticles.compute(str(s)) for s in mandelstams(6)}>>> sols = solve_scattering_equations(6, num_ss)
>>> len(sols)
6
>>> sols[0]
{'z3': mpc(real='#nbr', imag='#nbr'),
'z4': mpc(real='#nbr', imag='#nbr'),
'z5': mpc(real='#nbr', imag='#nbr')}Recursion for the elimination theory matrix
$$
\mkern -24mu M_i=
\left(
\begin{array}{ccccccc}
M_{i-1} & M_{i-1}^{z_{i-3}} & 0 & \dots & 0 & 0\\
0 & M_{i-1} & M_{i-1}^{z_{i-3}} & \dots & 0 & 0\\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots\\
0 & 0 & 0 & \dots & M_{i-1} & M_{i-1}^{z_{i-3}}\\
\end{array}
\right), \quad
M_4=H, \quad
H =
\left(
\begin{array}{c}
h_1\\
h_2\\
\vdots\\
h_{n-3}\\
\end{array}
\right)
$$
$M_i$ is of dimensions $(i−4)×(i−3)$ when written in terms of $M_{i−1}$. After a derivative is taken the relevant $z_i$ is assumed to be set to zero.
B 3. CHY-Integrands
Quick recap
Recall the expression for the amplitudes:
$\textit{A}_n \, = \, z_1^4 \cdot i \sum_{j = 1}^{(n-3)!} \frac{I_{\scriptscriptstyle CHY}(z^{(j)}(k); k; ϵ)}{\det(ϕ_{rst}^{ijk})(z^{(j)}(k); k)}$
So far:
$\circ\mkern -10mu \checkmark$ Theory independent part $z^{(j)}(k)$.
$\circ\mkern -10mu ✗$ Theory dependent part $I_{\scriptscriptstyle CHY}(z^{(j)}(k); k; ϵ)$.
First of all, note that $I_{\scriptscriptstyle CHY}$ must come with
four powers of $z_1=\infty$ in the denominator.
Summary of considered theories
| |
|
||||
| $Pf'(Ψ)$ | $C_n$ | $Pf'(A)^2$ | $W_1$ | ||
| $I_{\scriptscriptstyle CHY}$ | $Pf'(Ψ)$ | EG | YM | BI | CG |
| $C_n$ | YM | BS | NLSM | $(DF)^2$ | |
| $Pf'(A)^2$ | BI | NLSM | Galileon | ? | |
| $W_1$ | CG | $(DF)^2$ | ? | ? | |
Table: Possible QFTs built out of $Pf’(Ψ)$ , $C_n$ , $Pf’(A)^2$ and $W_1$.
A product is implied between rows and columns, eg: $I_{\scriptscriptstyle CHY, EG} = Pf’(Ψ) × Pf’(Ψ)$.
Definitions (scalars)
The Parke-Taylor-like factor $C_n$ is defined as:
$ C_n = \frac{1}{(z_1 - z_2) \dots (z_n - z_1)} $
Theories involving this factor are color ordered.
The $W_1$ factor from [29]:
$ W_1 = ∏_{i \in A} ω_i \;, \quad \text{with} \quad ω_i = \sum\limits_{j \in A \backslash \{i\}} \frac{ϵ_i \cdot k_j \, (z_j - z_r)}{(z_r - z_i)(z_i - z_j)} \;, \;\; r ≠ i. $
Definitions (matrices)
$$
\Psi_{2n\times2n}^{\text{anti-sym.}} =
\left(
\begin{array}{cc}
A_{n\times n} & -C^T_{n\times n}\\
C_{n\times n} & B_{n\times n}
\end{array}
\right),
\quad\quad
A_{ab} =
\begin{cases}
\frac{2 k_a \cdot k_b}{(z_a - z_b)} & a \neq b \; ,\\
0 & a = b \; ,
\end{cases}
$$
$$
B_{ab} =
\begin{cases}
\frac{2 ϵ_a \cdot ϵ_b}{(z_a - z_b)} & a \neq b \; ,\\
0 & a = b \; ,
\end{cases}
\quad\quad
C_{ab} =
\begin{cases}
\frac{2 ϵ_a \cdot k_b}{(z_a - z_b)} & a \neq b \; ,\\
- \sum\limits_{j \in A \backslash \{a\}} \frac{2 ϵ_a \cdot k_j}{(z_a - z_j)} & a = b \; .
\end{cases}
$$
The Pfaffian
The determinant of anti-symmetric matrices can be written as the square of a polynomial. This polynomial is called the Pfaffian.
$
\text{e.g.} \quad A = \left(
\begin{matrix}
0 & a \\
-a & 0
\end{matrix}
\right) \, , \quad
\det(A) = a ^ 2 \, , \quad
\text{Pf}(A) = a
$
Note: non trivial to get the Pfaffian from the determinant,
due to sign ambiguity.
The reduced Pfaffian
The matrices $A$ and $\Psi$ have two null vectors,
therefore their determinant and Pfaffian are zero.
Instead use:
$ \text{Pf’}(\Psi) = \frac{(-1)^{i+j}}{z_i - z_j} \text{Pf}(\Psi_{ij}^{ij}) \; , $
$\Psi_{ij}^{ij}$ denotes deletion of rows and columns $i$ and $j$.
An easy identity to spot
Born-Infeld, non linear sigma model and Galileon amplitudes involve the Pfaffian of the $n\times n$ matrix $A$.
The Pfaffian of an odd-size matrix is zero,
meaning in these theories only even point functions are non-vanishing.
More specifically, for Born-Infeld amplitudes this is a consequence of helicity conservation.
4. Amplitudes
Numerical amplitudes
We now have all the building blocks to compute amplitudes.
With the open source packages this is straightforward:
>>> from seampy import theories, NumericalAmplitude
>>> from lips import Particles
>>> theories
[YM, EG, BS, BI, NLSM, Galileon, CG, DF2]
>>> oDF2Amp = NumericalAmplitude(theory="DF2", helconf="+++++")
>>> oParticles = Particles(5)
>>> oDF2Amp(oParticles)
mpc(real='#nbr', imag='#nbr') Analytical reconstruction
Using the same strategy previously discussed we can reconstruct analytical expressions. For example:
$$
\begin{gathered}
A_{(\text{DF})^2}(1^+,\,2^+,\,3^+,\,4^+,\,5^+) =\\
\frac{i[12]⟨13⟩⟨25⟩[35]^2}{⟨12⟩^2⟨34⟩⟨45⟩}+\frac{i[14][24][35]}{⟨12⟩⟨35⟩}+\\
(12345 → 23451)\,+\,(12345 → 34512)\,+\\
(12345 → 45123)\,+\,(12345 → 51234)\,+\\
\frac{2i[15][23]⟨4|1+2|4]}{⟨12⟩⟨34⟩⟨45⟩}+\\
\frac{2i[12][45]⟨3|1+5|3]}{⟨15⟩⟨23⟩⟨34⟩}+\\
\frac{2i[12][15][34]}{⟨23⟩⟨45⟩}\phantom{+}
\end{gathered}
$$
Summary
1) Spinor-helicity rational coefficients can be reconstructed using:
$\circ$ singular limits for to the least common denominator;
$\circ$ doubly singular limits for partial fraction decompositions;
$\circ$ generic ansatze in singular limits for numerators;
Applications involve tree-level, one-loop and two-loop expressions alike.
2) Amplitudes in the CHY formalism can be computed via:
$\circ$ the scattering equations, numerically solved via elimination theory;
$\circ$ CHY-Integrads, which make manifest relations between theories;
Analytical expressions are then accessible using the above strategy.
Outlook
Application to the following quantities is well within reach:
$\circ$ six-parton one-loop amplitudes;
$\circ$ five-parton two-loop amplitudes;
for which we have already reconstructed several components.
Additionally it might be of interest to:
$\circ$ implement analytical expressions on GPGPU for fast evaluations;
$\circ$ reconstruct the seven-gluon one-loop coefficients;
$\circ$ assemble the NNLO three-jets cross-section;
$\circ$ apply the reconstruction technique to double copy structures.
Thank you for your attention!
Questions?